<><><><><><><><>

Pour les plus motivés, nous proposons des projets 3D.

La librairie G3D

Pour les plus motivés, nous proposons des projets 3D.

Le repère 3D

Axes et origine

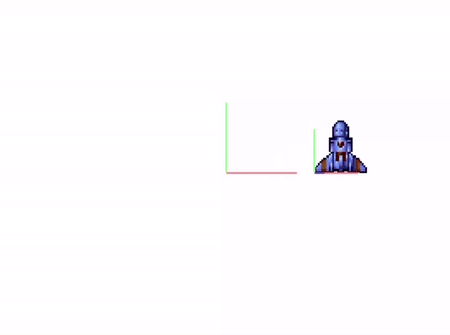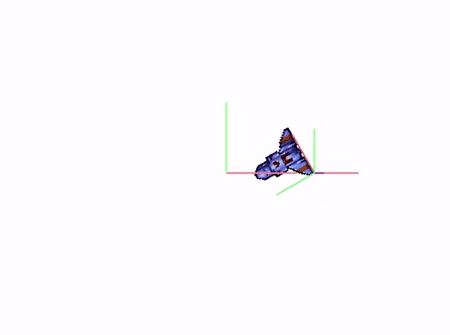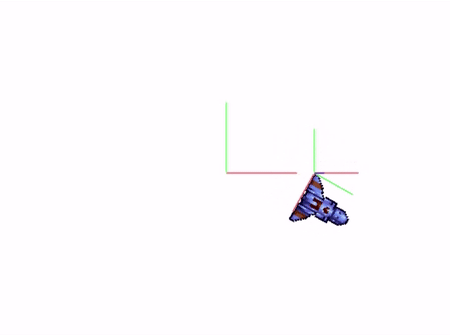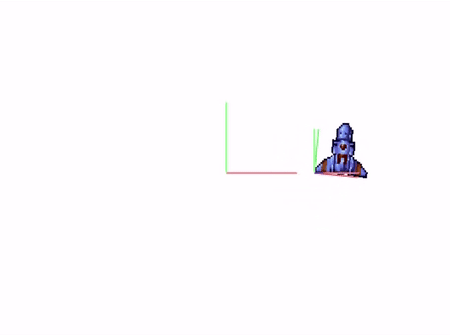
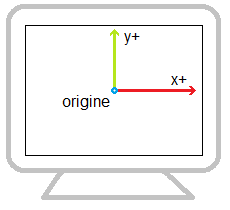
Par convention l’origine du monde est placée au milieu de la fenêtre de jeu. L’axe des abscisses et des ordonnées sont orientés comme dans le plan c’est à dire vers la droite et vers le haut. Le repère est direct, ainsi, la direction du 3ème vecteur doit correspondre au produit vectorie i^j. Ainsi l’axe de la profondeur est orienté vers la caméra (vers vous) :

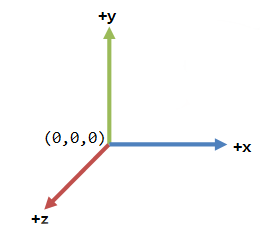
Attention cependant, comme l’axe des z est orienté vers la caméra est que la caméra est centrée sur le milieu de l’écran, l’axe des z est visuellement réduit à un point. Par convenction, on dessine l’axe des x, y et z en rouge, vert et bleu. Voici la vue depuis l’application :

La perspective

La mise en place d’une caméra produit un effet de perspective 3D. Par conséquent, des objets éloignés peuvent avoir la même taille que des objets plus petits mais plus proches de la caméra.

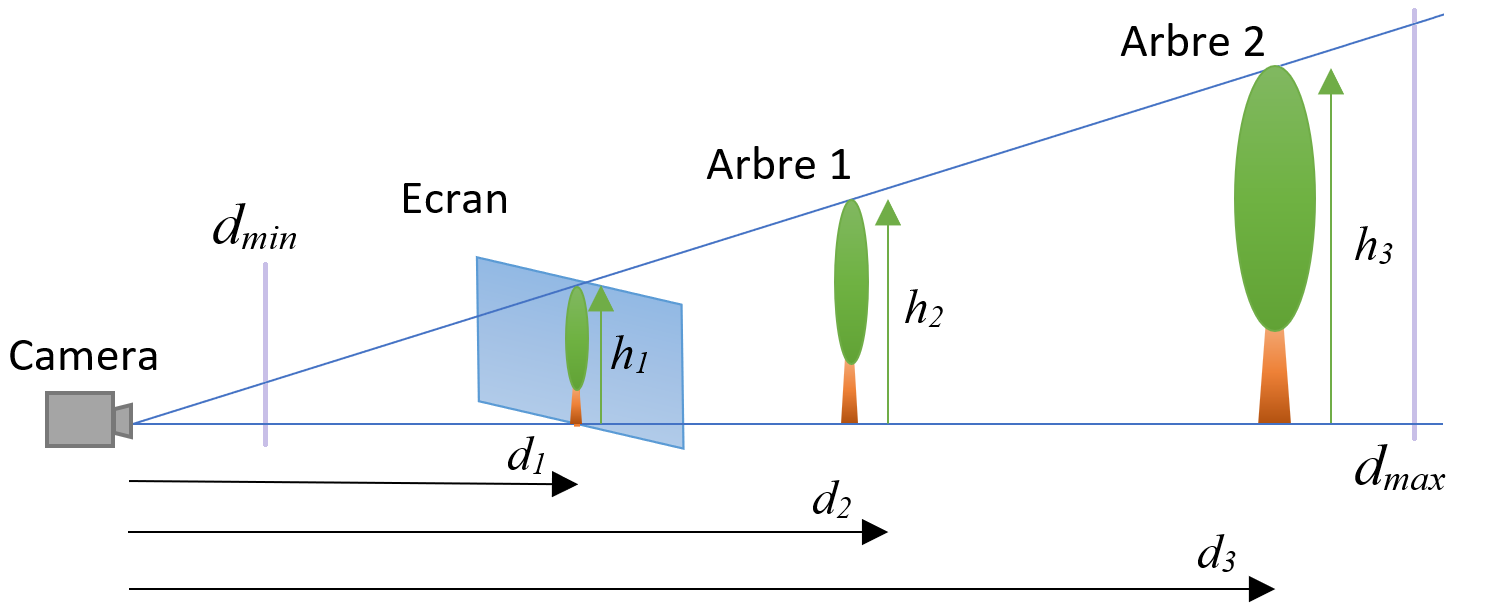
La formule mathématique qui modélise ce phénomène est la formule de Thalès (mathématicien contemporain de Pythagore), cette formule donne pour cet exemple :

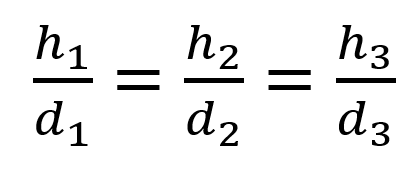
Rassurez-vous, vous n’allez pas effectivement tous les calculs de projection, la librairie prend cela en charge directement. Cependant, cette formule implique une contrainte technique dans la chaîne de calcul. En effet, si la distance d’un élément à la caméra est égale à 0, alors se produit une erreur de division par zéro. Pour éviter cela, on met en place une distance minimale à la caméra (znear) en-dessous de laquelle les éléments sont purement et simplement ignorés. La valeur de cette distance minimale doit donc toujours être strictement > 0. On prend généralement 1 ou 0.1. Un autre aspect pratique est la distance maximale à la caméra. En effet, d’après la règle sur la perspective, plus un objet est plus il est petit. Ainsi, il est inutile de perdre du temps à effectuer un rendu d’un objet éloigné. Par conséquent, au-delà de cette distance, les éléments sont tout simplement ignorés car considérés comme trop éloignés.

Note

Pour la petite histoire, lors d’un voyage en Egypte, Thalès de Milet aurait mesuré la hauteur de la pyramide de Kheops par un rapport de proportionnalité avec son ombre : « Le rapport que j’entretiens avec mon ombre et le même que celui que la pyramide entretient avec la sienne. »

Hiérarchie de repères

Pour organiser une scène 3D, on peut donner les coordonnées de tous les objets en absolue, c’est à dire par rapport au repère d’origine. Cependant, cela devient vite difficile lorsque l’on commence à vouloir déplacer ou à faire tourner des objets les uns par rapport aux autres. Il est alors plus simple d’utiliser un système nodal de repères et de sous-repères. Le système nodal correspond à un arbre dont la racine est l’origine avec les 3 axes principaux. Chaque branche de l’arbre amène vers un nouveau noeud qui correspond à un sous-repère ayant subi une translation OU une rotation par rapport à son repère parent. La fin d’une branche contient un ou plusieurs objets dont les coordonnées sont exprimées par rapport au repère local.

Si vous avez du mal avec cette description, pensez à un robot dont vous décrivez la trajectoire. Par exemple, si vous ordonnez : 1- avance puis 2- tourne sur la gauche de 90°. Le premier déplacement se fait dans la direction où il regarde. La rotation qui suit se fait par rapport à sa nouvelle position et non par rapport à la position de départ. Si vous lui demandez ensuite d’avancer (nouvelle translation), il avancera par rapport à sa position/rotation courante.

Gardez en mémoire, que lorsque vous êtes sur un noeud particulier, un sous-repère, la connaissance des repères précédents n’est pas utile pour déterminer ce qui se passe ensuite. En effet, comme toutes les opérations sont décrites par rapport au repère courant, chaque fois que l’on applique une transformation pour créer une nouvelle position/rotation, on peut oublier le repère parent.

Lorsque l’on arrive à la fin d’une branche, il semble peut intéressant de refaire les opérations inverses pour retrouver la position du repère une ou plusieurs branches avant. Avant de simplifier les opérations, la librairie fournit deux fonctions très utiles :

Push() sauvegarde en mémoire le repère courant

Pop() extrait le dernier repère sauvegardé et le substitue au repère courant

Les fonctions permettant de gérer les transformations de repère sont :

Rotate(float angleDeg, V3 axis) : déclenche une rotation autours de l’axe donné en paramètre.

Translate(V3 v) : applique une translation d’un vecteur v.

Scale(V3 zoom) : déclenche un changement d’échelle sur chaque direction, un coefficient par direction x/y/z.

Exemple 1

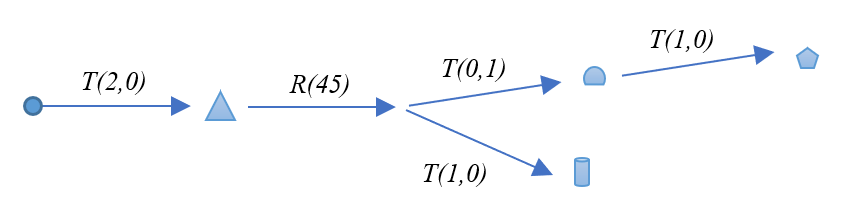
Nous présentons le résultat obtenu par une série d’opérations de transformation et de dessin :

Translation(2,0) : le repère courant se déplace sur son axe x+ d’une distance de 2.

Draw( ) : dessin d’un triangle pointant dans la direction y+ (repère local).

Rotation(+45°) : le repère courant effectue une rotation de 45° dans le sens trigonométrique.

Push( ) : la position/orientation du repère courant est sauvegardée.

Translation(0,1) : le repère courant avance de 1 suivant son axe y+.

Draw( ) : une demi-sphère est dessinée avec son diamètre sur l’axe des x (repère local).

Translation(1,0) : le repère courant se déplace suivant son axe x+ d’une distance de 1.

Draw( ) : dessin d’un polygone.

Pop( ) : le repère courant est oublié, on rappelle le dernier repère sauvegardé.

Translation(1,0) : le repère courant se déplace d’une unité dans sa direction x+.

Draw( ) : dessin d’un cylindre dont l’axe est orienté suivant l’axe y+ du repère local.

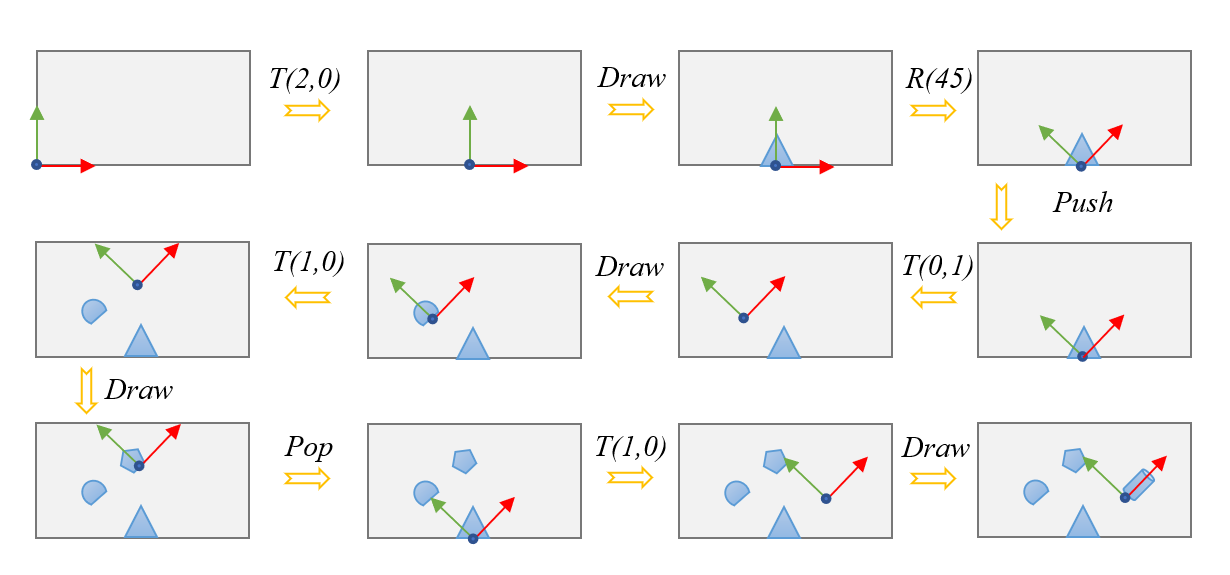
L’arbre des transformations associées à cette construction est réprésenté ainsi :

Exemple 2

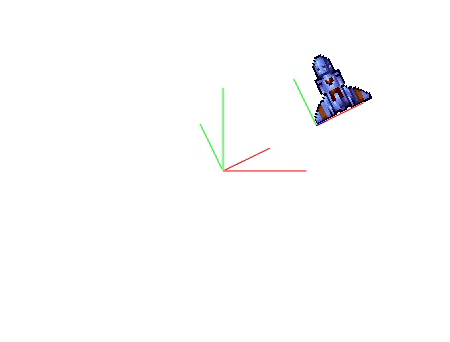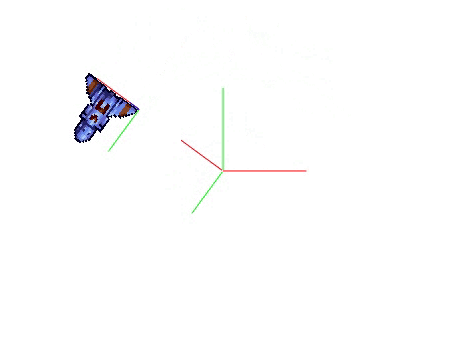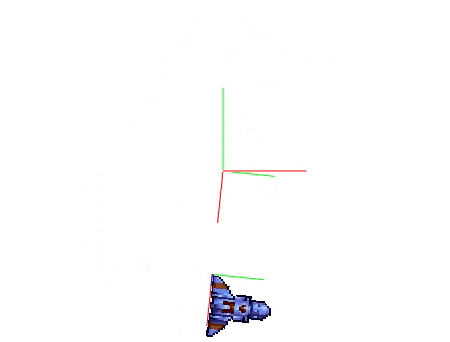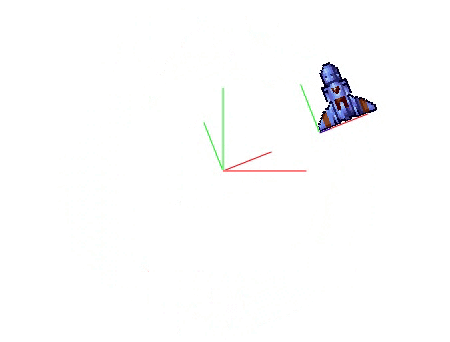
Nous rappelons que deux rotations successives sont équivalentes à une seule rotation. De même, deux translations successives se résument à une seule translation. Cependant, on ne peut pas permuter une rotation et une translation, les résultats obtenus sont différents. Reprenons le vaisseau de Xenon. Nous utilisons :

Une rotation de α.t degrés, t variant avec le temps.

Une translation de (2,0)

Voici les résultats suivant l’ordre choisi pour ces transformations :

Rotation(t) → Translation(2,0) → Draw()	Translation(2,0) → Rotation(t) → Draw()

Texturing

Les coordonnes uv

A la base une texture est une surface dont on va se servir pour colorier nos surfaces. En production, on utilise différentes tailles de texture pour représenter le même objet. En effet, lorsque l’objet est éloigné et fait une taille de 30 pixels de haut à l’écran, une texture 64x64 est largement suffisante. Lorsque nous sommes plus proches de cet objet, sa taille à l’écran peut être de 600 pixels. Si l’on conserve la texture basse résolution, on va devoir l’étirer pour recouvrir la surface à afficher. On va ainsi faire apparaître des gros pixels ! Ainsi, il faudrait utiliser idéalement une texture de 512x512.

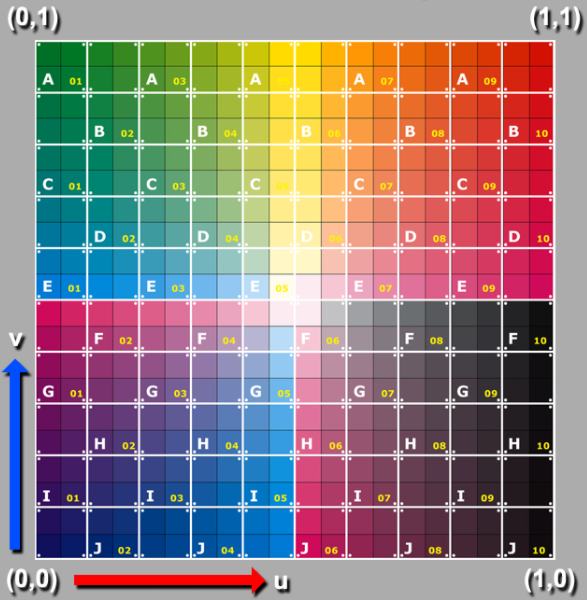
Il nous faut donc mettre en place un système de coordonnées qui soit indépendant de la résolution de la texture. Nous allons pour cela utiliser les coordonnées uv pour nous repérer sur une image. Les uv sont similaires aux coordonnées (x,y), sauf que ce terme est dédié au texture. Ainsi dès que l’on parle d”uv, on sait qu’on traite une position dans une image. Les coordonnées uv sont par convention toujours la plage [0,1]x[0,1] quelles que soient les dimensions de l’image. Voici une texture sur laquelle on a superposé la grille de coordonnées uv :

Correspondance

Maintenant, chaque sommet d’une face va être associé à :

Des coordonnées (x,y,z) dans l’espace 3D

Des coordonnées (u,v) dans la texture.

Ainsi, lorsqu’un tel sommet est dessiné à l’écran, il aura comme couleur la couleur du pixel présent dans la texture aux coordonnées (u,v) données. Prenons la texture d’un dés 6 faces :

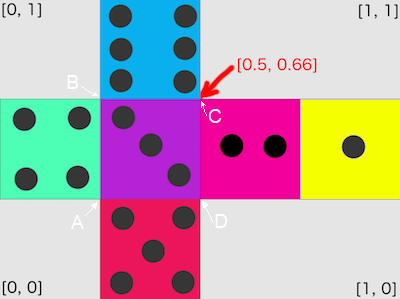
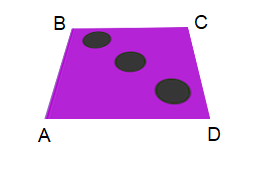
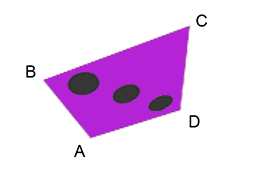
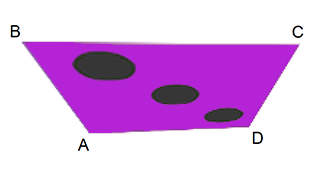
Prenons l’exemple d’un rectangle ABCD dans l’espace, si nous associons à chaque point une coordonnée uv :

A : (1/4,1/3) pour le point en bas à gauche

B : (1/4,2/3) pour le point en haut à gauche

C : (1/2,2/3) pour le point en haut à droite

D : (1/2,1/3) pour le point en bas à droite

Alors suivant différentes positions des points A, B, C et D, le rendu sera le suivant :

C’est à la carte graphique d’effectuer les calculs de déformation pour que la texture s’adapte à la forme du quadrilatère ABCD.

Primitives géométriques

Dans le monde de la 3D temps réel, les cartes graphiques utilisent principalement des surfaces décrites à partir de facettes ayant la forme de triangle. Pour représenter les primitives géométriques (sphère, tore, cylindre), il faut donc échantillonner des points sur ces surfaces puis les relier entre eux pour former des facettes.

Par convention, nous allons utiliser les équations paramétriques de la sphère et du cylindre de telle sorte que le point associé aux paramètres (0,0) soit au milieu à gauche.

Cylindre

Nous cherchons à représenter un cylindre d’hauteur H et de rayon R :

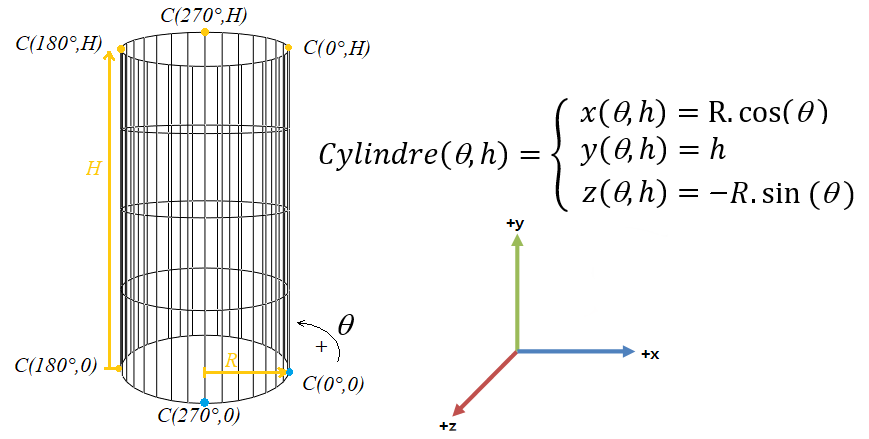
Dans quelle plage de valeurs évolue l’angle θ ? Il faut échantillonner toute la surface, l’avant aussi bien que l’arrière. Pour cela nous vous proposons de faire varier θ dans l’intervalle [0,360]. Le paramètre h, pour atteindre le haut et bas du cylindre doit parcourir la plage de valeur [0,H]. Il reste ensuite à choisir un pas d’échantillonnage :

Pour l’angle angle θ : 10 degrés, par exemple

Pour la hauteur : H/4 pour obtenir 4 tronçons.

Nous avons le code de principe suivant :

dθ = 10
dh = H/4
Pour θ allant de 0 à 360 par pas de dθ
        Pour h allant de 0 à H par pas de dh
                A = Cylindre(θ   ,h)
                B = Cylindre(θ   ,h+dh)
                C = Cylindre(θ+dθ,h+dh)
                D = Cylindre(θ+dθ,h)
                Créez les facettes (A,B,C) et (A,C,D)

Dans la figure ci-dessus, les facettes ont été représentées par paire ABC+ACD=>ABCD pour éviter de surcharger le schéma.

Note

Si vous cherchez le vecteur normal à la surface du cylindre au point Cylindre(θ,h), inutile de faire de longs calculs. En effet, par analogie avec le cercle où la normale à un point a la même direction que le rayon arrivant à ce point, la normale au point Cylindre(θ,h) est donnée par N(θ,h) = (cos(θ),0,sin(θ)).

Avertissement

Par rapport à la formule usuelle, remarquez l’apparition du signe - sur la composante en z. Cela vient du fait que le repère n’est pas le repère usuel et que la formule a été modifiée pour caler le point (0,0) à droite et pour que l’angle θ+ soit orienté dans le sens trigonométrique.

Pour recouvrir le cylindre d’une texture, comme une canette de soda par exemple, il reste à effectuer une correspondance entre :

La plage des valeurs de θ : [0,360], avec la plage des valeurs de u : [0,1]

La plage des valeurs de h : [0,H], avec la plage des valeurs de v : [0,1]

Nous vous laissons les formules de correspondance en exercice.

Sphère

Comment modéliser une sphère ? On peut représenter un point sur une sphère de centre (0,0,0) et de rayon R par la formule suivante :

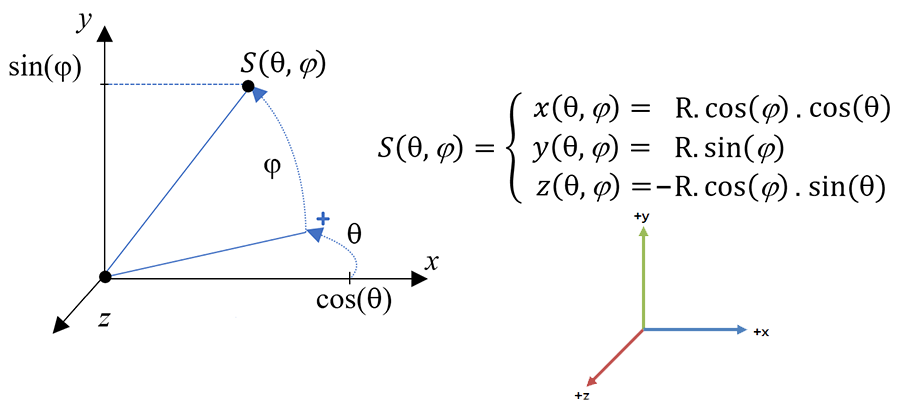
Il faut ensuite identifier une plage de valeurs pour les angles θ et φ. Pour cela, nous vous proposons de faire varier θ dans l’intervalle [0,360]. Cela permet de parcourir l’équateur de la sphère lorsque φ=0. Il reste ensuite à faire varier φ pour atteindre les deux pôles. Pour cela, on utilise la plage de valeurs [-90,90]. Il vous reste ensuite à choisir un angle servant de pas d’échantillonnage : de 10 degrés par exemple. Nous avons le code de principe suivante :

da = 10
Pour φ allant de -90 à 90 par pas de da
        Pour θ allant de 0 à 360 par pas de da
                A = S(θ,φ)
                B = S(θ,φ+da)
                C = S(θ+da,φ+da)
                D = S(θ+da,φ)
                Créez les facettes (A,B,C) et (A,C,D)

Pour recouvrir la sphère d’une texture, comme une carte du monde par exemple, il reste à effectuer une correspondance entre :

La plage des valeurs de θ : [0,360], avec la plage des valeurs de u : [0,1]

La plage des valeurs de φ : [-90,90], avec la plage des valeurs de v : [0,1]

Nous vous laissons les formules de correspondance en exercice.

La fonction DrawBorder()

La fonction DrawBorder() disponible dans la librairie G3D permet de dessiner les contours des facettes, y compris les facettes colorées ou texturées. Vous pouvez ainsi l’utiliser pour faire des rendus en fil de fer ou pour contrôler vos maillages. Deux fonctions sont disponibles :

void DrawBorder(V3 A, V3 B, V3 C, float thickness = 2, Color EdgeColor = Color::White);

void DrawBorder(V3 A, V3 B, V3 C, V3 D, float thickness = 2, Color EdgeColor = Color::White);

La première version permet de dessiner une facette-triangle ABC et la deuxième version permet de regrouper deux facettes-triangles pour dessiner un Quad (groupe de 4 sommets). Voici deux exemples ci-dessous :

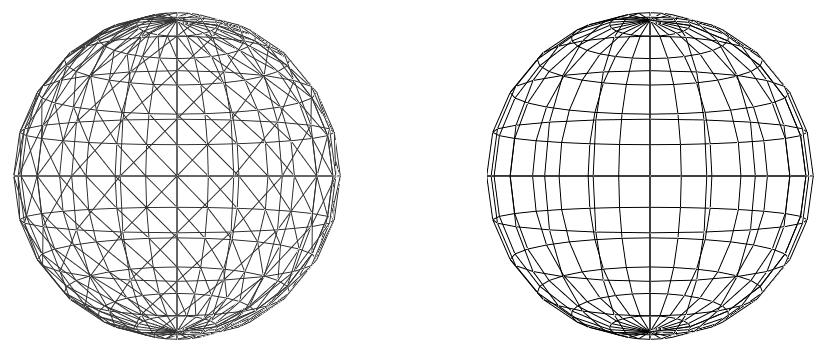
Chacune de ces fonctions prend en paramètres l’épaisseur du trait qui peut être inférieure à 1 pour apparaître très fin mais vous pouvez aussi choisir une valeur pour donner un rendu aux contours épais.

Illumination

Les lampes de la scène

L’éclairage de la scène est utilise deux lampes :

Une lampe blanche, intensité 80%, simulant l’éclairage du soleil. Elle est placée sur le côté de la caméra en haut à droite.

Une lampe ambiante blanche, intensité 20%, éclairant toutes les surfaces.

La lampe évite l’apparition de zones noires correspondant aux zones non éclairées par la lampe principale que l’on trouve généralement à l’arrière des volumes.

Le modèle d’illumination

Lorsque l’on étudie la couleur d’un objet, on considère un point précis dans l’espace. Ce point reçoit des rayons lumineux. On peut ainsi calculer la couleur émise par ce point. Le comportement de la lumière le plus courant dans le monde physique est la diffusion : un rayon lumineux en tapant sur une surface est réémis dans toutes les directions. Ainsi, la réflexion diffuse ne varie pas en fonction de l’endroit où on regarde l’objet. L’intensité de la lumière perçue est uniquement fonction l’angle entre le vecteur lumière et le vecteur normal à la surface :

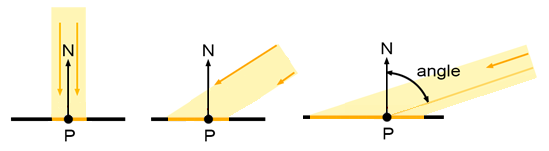
Ainsi, plus un rayon lumineux est rasant, plus il éclaire une surface importante. Par conséquent l’énergie lumineuse portée par le rayon étant la même, la surface éclairée sera moins lumineuse. L’angle pour lequel l’intensité est maximale correspond à la configuration où le vecteur normal N et le vecteur lumière L sont colinéaires.

La librairie graphique et le carte GPU se charge d’effectuer les calculs d’illumination. Cependant, pour qu’elles puissent simuler le comportement de la lumière, il faut leur fournir un vecteur normal qui constitue le point d’entrée de tous les calculs de simulation de la lumière.

Vecteur normal

Nous ne sommes pas en mesure d’appliquer les formules de dérivations sur des maillages (surfaces facettisées).

Pour rappel, le vecteur normal N(u,v) d’une surface paramétrique S(u,v) s’obtient par le produit vectoriel des deux dérivées partielles au point courant. Ainsi le vecteur N(u,v) correspond à la normalisation du vecteur ∂S/∂u(u,v)^∂S/∂v(u,v). Les deux vecteurs ∂S/∂u(u,v) et ∂S/∂v(u,v) étant tangents à la surface au point S(u,v), le produit vectoriel permet de construire un vecteur perpendiculaire au plan tangent :

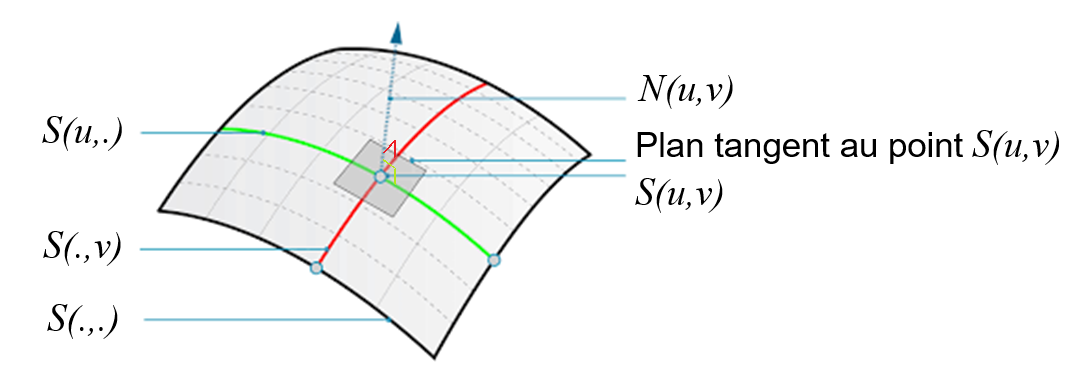
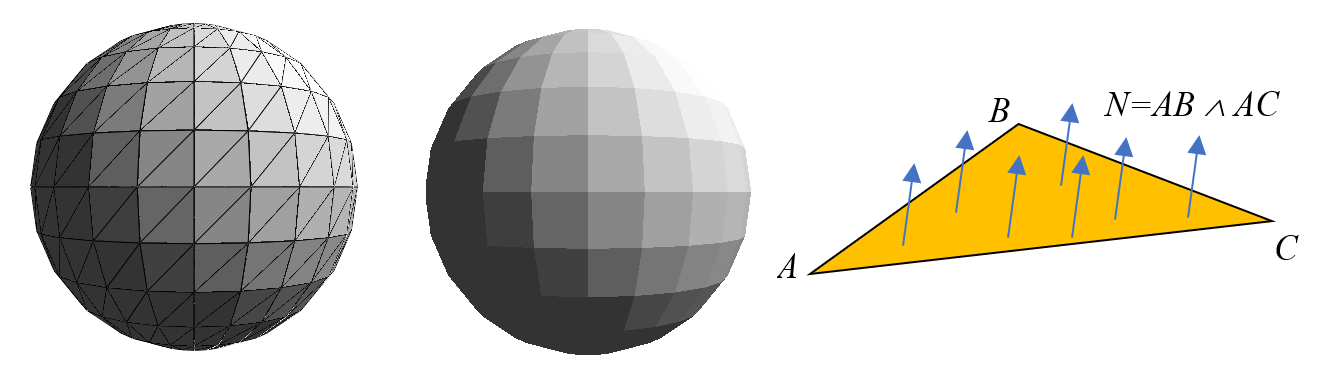
Pour calculer le vecteur normal à une facette triangulaire ABC, on peut, dans la même logique que précédemment, calculer le produit vectoriel de deux de ses côtés : AB^AC. Dans ce contexte, le vecteur normal sera constant pour tout point sur la facette. Par conséquent l’intensité lumineuse produite par la lampe sera identique pour tous les points. Graphiquement, ce choix a pour effet de créer un rendu de type facettes de diamant :

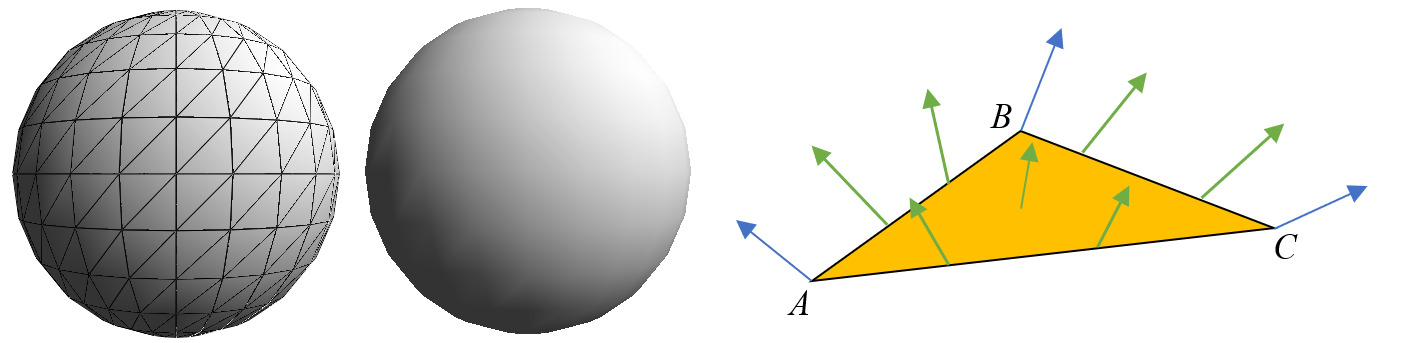
Une deuxième option existe. Au premier abord, elle est assez déroutante car elle consiste à associer un vecteur normal à chaque point ! C’est assez délicat car habituellement on associe la notion de normale à une surface. Mais ici, l’idée est que l’on perçoit les objets du monde réel à partir d’un échantillonnage de points. On peut donc considérer que l’on a aussi échantillonné les normales de ces points dans le monde réel. Ainsi, notre facette est maintenant composée de trois points chacun ayant sa propre normale. Elles seront souvent différentes : pensez à des points échantillonnés sur une sphère. Pour les points à l’intérieur de la facette, la carte graphique va effectuer une approximation de la normale en fonction des trois normales des sommets. Dans le graphique ci-dessous, les approximations des normales sont présentées en vert. Lorsque l’on se rapproche d’un des sommets, la normale calculée est très proche de celle du sommet adjacent. Si l’on se place sur le point central de la facette, la normale correspondra à une moyenne des trois normales des sommets. Le résultats sont assez convaincants ! Par exemple pour une sphère, même si la géométrie apparaît clairement comment étant celle d’un polyèdre, le dégradé lumineux est très proche d’une sphère réelle :

Texturing

Il est bien sûr possible de rajouter une texture qui sera combinée avec ces effets d’éclairage. Voici une illustration montrant les trois rendus : sans éclairage, facettisé et dégradé :

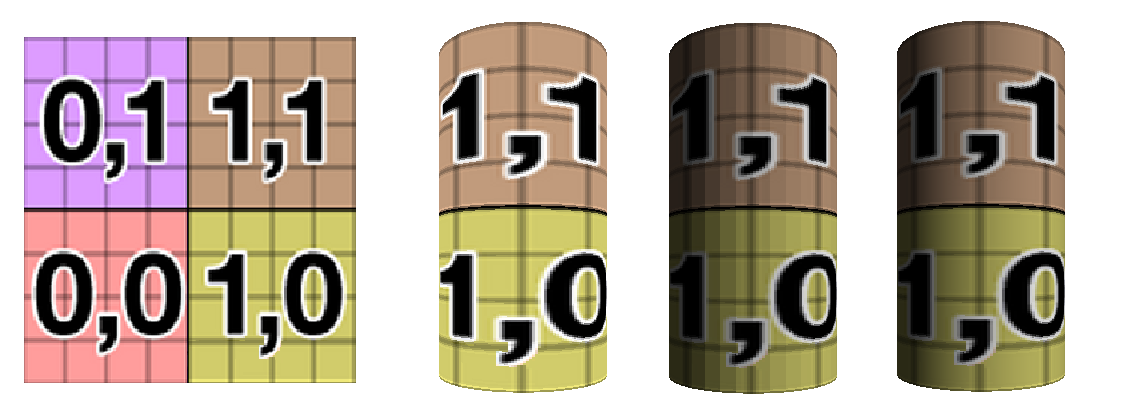
Note

La texture est une texture de test de calage pour les uv. Elle est présentée sur la gauche. La moitié gauche de cette texture est utilisée pour recouvrir l’arrière du cylindre, elle n’est donc pas visible. N’oubliez pas que nous partons de la droite et que nous tournons dans le sens trigonométrique. La partie droite de la texture recouvre donc la face avant du cylindre.

TFace

La librairie G3D offre une structure TFace (Triangular Face) simplifiant les manipulations de textures et de normales. Pour la gestion des textures, les fonctions suivantes sont disponibles :

SetColor(Color Color) : permet de fixer une couleur unique pour la facette

SetTexture(int IdTexture, uv uA, uv uB, uv uC) : associe une id de texture à cette face pour la recouvrir. Dans cette configuration, il faut obligatoirement passer les coordonnées uv des trois sommets.

A noter qu’en l’absence d’information, la facette sera blanche.

Pour la gestion des normales, les fonctions suivantes sont accessibles :

SetFaceNormal(V3 N) : associe un vecteur normal unique pour la facette. Cela déclenche le rendu en mode facetisé.

SetVertexNormal(V3 nA, V3 nB, V3 nC) : associe un vecteur normal à chaque sommet. Cela déclenche le rendu en mode dégradé de lumière.

Par défaut, il n’y a pas d’application des lumières sur la surface.

Note

Le 3ème mode sans éclairage est utile pour représenter des sprites à l’écran. Il vous permet d’afficher l’image exacte du sprite sans tenir compte de l’effet des lumières.

Gestion de la profondeur

Depth-test

Lors du rendu des différents objets, vous vous apercevrez que les objets à l’avant recouvrent les objets placés derrière. Comment les cartes 3D gèrent-elles cela ? En fait, l’algorithme appelé Z-buffer est très simple. En parallèle de la matrice des pixels de l’écran est créée une matrice de même taille qui va stocker la composante en z de chaque pixel affiché dans la matrice de pixels. Ainsi, lorsque l’on veut afficher un nouveau pixel à la position (x,y), on va d’abord lire dans le Z-buffer la composante en z du pixel de coordonnées (x,y). Si la composante en z du pixel déjà affiché est inférieure à celle du nouveau pixel, le nouveau pixel est donc plus proche de la caméra. Par conséquent, on affiche ce nouveau pixel : la couleur du pixel est stockée dans la matrice de pixels et sa composante en z est stockée dans la matrice des profondeurs.

La transparence

Il est possible d’utiliser des textures avec transparence comme on a pu le faire en 2D. Cependant, c’est peu compatible avec l’algorithme du Z-buffer. En effet, pour calculer le résultat d’une transparence, il faut connaître l’objet juste derrière afin de mélanger les couleurs. Pour cela, il faudrait trier les objets par ordre de profondeur. Or, l’algorithme du Z-buffer est un algorithme qui ne gère pas cet ordre-là. En effet, il traite les facettes par ordre d’arrivée. Par conséquent, dès que vous voulez utiliser de la transparence, il faut faire très attention, car les résultats sont souvent bogués.

Dessiner des Font

En cours…

Exercices

Exercice 1

Représentez un dé :

Construisez un cube à six faces pour modéliser un dé de jeu de société.

Appliquez lui une : texture en croix ou une autre texture de votre choix.

Calculez les uv correspondant.

Utilisez le modèle avec une normale par face.

Attention, suivant la face à laquelle il appartient, un sommet peut avoir des coordonnées uv complètement différentes.

Exercice 2

Représentez la terre :

Construisez une sphère.

Trouvez une texture de mappemonde et convertissez-la en ppm.

Calculez les uv correspondants.

Utilisez le modèle avec une normale par sommet pour obtenir un dégradé.

Exercice 3

Représentez une boule de billard.

Construisez une sphère.

Créez sous mspaint une texture couleur unie avec un chiffre au milieu dans un rond blanc.

Calculez les uv correspondants.

Utilisez le modèle avec une normale par sommet pour obtenir un dégradé.

Calez votre texture pour que le chiffre soit centré sur l’équateur de la sphère. S’il est aux pôles, il va être écrasé.

Déplacez la sphère de gauche à droite par translation.

Appliquez une rotation sur la sphère pour qu’elle tourne en même temps qu’elle se déplace.

Calez la rotation et le déplacement pour qu’un tour complet corresponde à une translation de 2πR.