L’apprentissage
La question légitime qui interpelle tout élève est la suivante : comment une machine peut-elle apprendre ? Nous allons répondre à cette question et présenter quelques notions clefs utilisées dans l’apprentissage automatique.
Une IA = une fonction mathématique
Comment sont représentées les informations dans un problème d’apprentissage ?
En entrée, nous pouvons analyser :
Une image représentée sous la forme d’un tableau de valeurs 8 bits allant de 0 à 255.
Un son modélisé par une suite de valeurs issues de l’enregistrement depuis un micro.
Un jeu. Par exemple dans Pac-Man, les informations correspondent à la position du héros et des fantômes, au score et à la carte.
En sortie, on peut estimer :
Un âge
Un score
Une probabilité
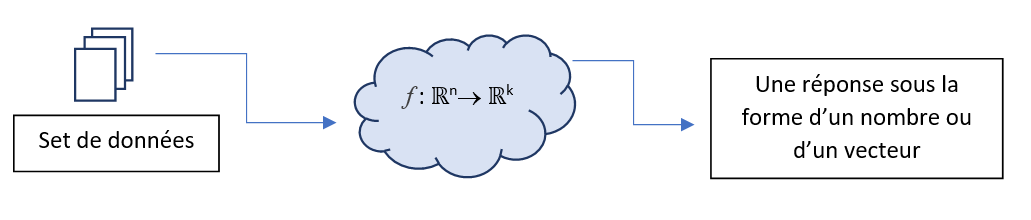
Ainsi, les informations en entrée et en sortie prennent la forme de nombres. Par conséquent, construire une IA traitant \(n\) valeurs numériques en entrée pour produire \(k\) valeurs numériques en sortie, s’apparente à mettre en place une fonction mathématique \(f\) de \(\mathbb{R}^n\rightarrow \mathbb{R}^k\).
Note
Ceci a un impact immédiat sur le format des données. En effet, si nous modélisons notre IA par une fonction mathématique de \(\mathbb{R}^n\rightarrow \mathbb{R}^k\), cela implique que toutes les entrées doivent être de même taille. Ainsi, pour créer une base d’apprentissage sur des images, il faut les retailler et les redimensionner pour qu’elles aient toutes la même résolution. Dans la même logique, pour mettre en place une base d’apprentissage sur des phrases, il faudra compléter chaque phrase par des mots « vides » pour qu’elles aient toutes la même longueur.
Voici donc notre premier système :
Note
Les réseaux de neurones, que nous présenterons plus tard, permettent de générer ce type de fonctions.
Les paramètres d’apprentissage
Nous disposons d’une fonction \(f\) fournissant une réponse pour des informations fournies en entrée. Maintenant, nous voulons faire en sorte que cette fonction puisse évoluer sinon aucun apprentissage ne sera possible. Pour cela, nous allons ajouter des paramètres supplémentaires, dit paramètres internes ou paramètres d’apprentissage aussi appelés poids (weights en anglais). Ils vont être utilisés comme des entrées supplémentaires de la fonction \(f\) au même titre que les données à traiter, ainsi nous obtenons la modélisation suivante :
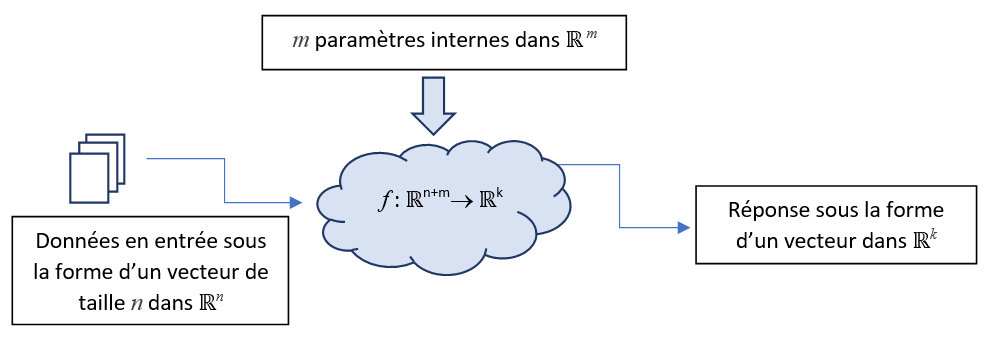
L’ajout de ces poids va permettre à notre système d’apprendre, en effet, si les réponses fournies par la fonction f sont incorrectes, on peut faire évoluer ces paramètres internes pour tenter d’obtenir une réponse éventuellement meilleure.
Ainsi, durant la phase d’apprentissage, les données en entrée sont des données « constantes » au sens où elles ne sont pas modifiées durant cette phase. La fonction f est choisie et conservée telle quelle durant toute la phase d’apprentissage. Les seuls éléments pouvant évoluer durant la phase d’apprentissage sont les paramètres internes.
Prenons un exemple basique. Supposons que nous avons une seule valeur en entrée notée \(x\). Prenons comme fonction \(f\) un polynôme du second degré de la forme \(f(x,a,b,c) = ax²+bx+c\) où \(a\), \(b\) et \(c\) représentent ses paramètres internes. Différentes valeurs pour ces paramètres internes fournissent des réponses différentes pour une même valeur en entrée \(x = 2\) :
Pour \(a = 1, b = 3\) et \(c = 5\), la réponse est égale à : \(f(x) = 2^2+3 \cdot 2+5 = 15\)
Pour \(a = 3, b = 1\) et \(c = 3\), la réponse est égale à : \(f(x) = 3\cdot 2^2 + 1\cdot 2+3 = 17\)
Note
Comment initialiser les paramètres internes en début d’apprentissage ? Impossible de répondre à cette question. Les paramètres sont donc initialisés aléatoirement par convention. Ainsi, en relançant un apprentissage, on obtient une IA différente.
L’apprentissage supervisé
Dans l’apprentissage supervisé, nous mettons en place une approche utilisant des vérités terrain : une base d’échantillons dont on connaît exactement les réponses qui vont servir de référence. Par exemple :
Pour l’évaluation de l’âge d’une personne à partir d’une photo, nous connaissons pour chaque image l’âge exact de la personne.
Pour la classification d’images, on dispose d’une base d’images ainsi que la catégorie associée à chaque image : chien, chat, grenouille…
Pour la description automatique d’images : on dispose d’une phrase décrivant le contenu de chaque image.
Pour la transcription automatique (Speech to Text), plusieurs phrases enregistrées à l’oral constituent la base d’apprentissage et pour chacune d’entre elles, nous connaissons sa transcription.
L’apprentissage supervisé, pour être efficace, doit disposer de plusieurs milliers d’échantillons en entrée. Plus la taille de l’échantillon de référence est importante, plus vous augmentez la qualité de l’apprentissage. On peut citer quelques bases annotées utilisées régulièrement dans la formation et la recherche :
MNIST : base d’images correspondant aux chiffres manuscrits de 0 à 9 ; utilisée à l’origine pour construire les machines automatisées de tri postal ; 60 000 images de résolution de 28x28 en niveaux de gris.
CIFAR10 : base d’images pour la classification d’images. 60 000 images, résolution de 32x32 en couleur, 10 classes : avion, voiture, oiseau, chat, daim, chien, grenouille, cheval, navire et camion.
CIFAR100 : 100 classes cette fois et 600 images par classe.
OXFOR102 : 102 classes de fleurs !
Fashion MNIST images en niveaux de gris sur de vêtements et autres articles de Zalando en 28x28.
FOOD 101 101 catégories, 1000 images/classe.
FGVC Aircraft 102 catégories, 10 000 images.
Birdsnap 500 espèces d’oiseaux, 100 images par catégories.
ImageNet : base d’images qui sert de référence pour le problème de classification : 1000 classes, plus d’un million d’images en couleur de taille variable.
COCO : base d’images pour la segmentation et la description d’images : 80 000 images accompagnées de leurs descriptions.
Vous pouvez consulter une liste exhaustives de bases d’apprentissage ici.
Note
L’apprentissage non supervisé est une thématique de recherche consistant à catégoriser, par exemple, des photos d’animaux sans connaissance à priori des espèces présentes sur les images.
La fonction d’erreur
Lorsque le système nous fournit une estimation, nous pouvons évaluer sa qualité en utilisant une fonction d’erreur notée \(FntErr()\) permettant d’indiquer si l’estimation est éloignée de la réponse attendue. Par convention, la fonction d’erreur doit être positive et sa valeur doit augmenter lorsque la réponse s’éloigne de la valeur recherchée.
Prenons comme exemple le problème de la détection de l’âge d’une personne. En utilisant une base d’images, nous connaissons, pour chaque image, l’âge de référence \(age_{ref}\) de la personne présente sur l’image. Nous notons l’âge estimé \(age_{est}\) par la fonction \(f\). Voici un exemple de fonction d’erreur que nous pouvons utiliser dans ce contexte :
Voici différents scénarios pour une même image en entrée où la personne a 37 ans :
Age estimé : 37, \(FntErr(...) = |37-37| = 0\) car on a trouvé la bonne réponse
Age estimé : 39, \(FntErr(...) = |37-39| = 2\) faible erreur, 2 ans trop vieux
Age estimé : 30, \(FntErr(...) = |37-30| = 7\) l’erreur augmente car l’écart augmente
Age estimé : 87, \(FntErr(...) = |37-87| = 40\) soit 40 ans trop vieux, l’erreur est forte
Note
Dans cet exemple, la valeur de l’erreur correspond à un nombre d’années. Mais rarement l’erreur aura une unité, nous ne saurons pas si 0.1 ou 150 correspond à une erreur importante ou non.
Nous constatons dans cet exemple que si l’erreur diminue, alors la qualité de la réponse augmente et réciproquement.
L’erreur d’un échantillon
Prenons un échantillon dans notre base d’apprentissage. Nous utilisons la fonction \(f\) pour obtenir une estimation et nous injectons cette réponse directement dans la fonction d’erreur \(FntErr()\) pour obtenir une évaluation de sa qualité :
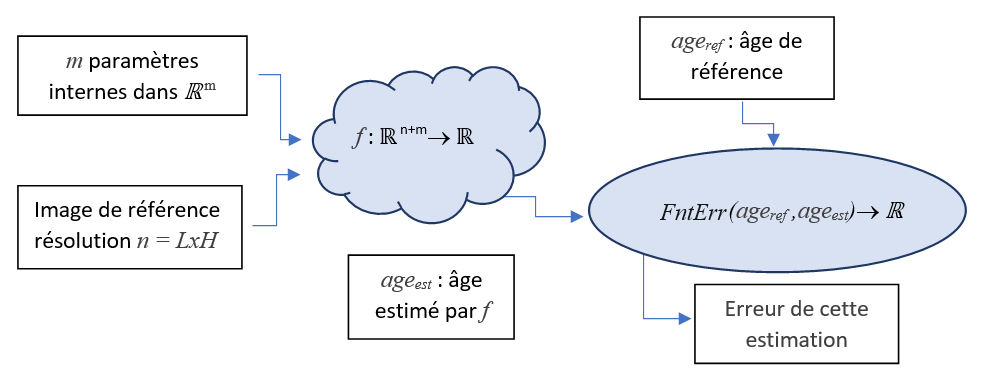
On peut donc construire une nouvelle fonction \(ErrEch()\) qui à partir d’un échantillon \(I\) donne directement l’erreur de l’estimation associée à cet échantillon :
Avec :
\(I\) : donnée en entrée (une image par exemple).
\(ref_I\) : réponse exacte associée.
\(f\) : fonction d’apprentissage.
\(w\) : paramètres d’apprentissage (weights).
L’erreur totale
Pour estimer l’erreur totale sur l’ensemble de la base d’apprentissage, nous construisons une troisième et dernière fonction \(ErrTot()\) servant à sommer les erreurs induites par chaque échantillon dans la base d’apprentissage :
L’optimum
Nous cherchons à minimiser la fonction \(ErrTot()\) par rapport aux paramètres internes \(w\). En utilisant notre algorithme naïf, nous descendons le long de cette pente chaque fois que de meilleurs paramètres internes \(w_i\) sont trouvés. Nous finissons par atteindre un minimum local dans lequel l’algorithme va stagner. Il est difficile de savoir à ce niveau comment sortir de cette zone pour trouver un meilleur optimum. On va souvent relancer la phase d’apprentissage à partir d’une autre position de départ pour espérer trouver un meilleur optimum.
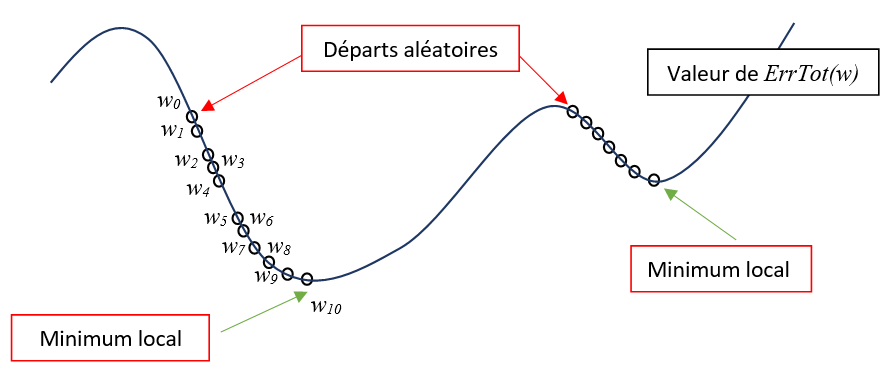
Ainsi, ni notre méthode d’optimisation naïve, ni aucune autre méthode d’optimisation ne peut garantir la convergence vers l’erreur minimale. En effet, il nous est impossible de déterminer un fois un minimum atteint, s’il s’agit d’un minimum local ou d’un minimum global.
Note
Vous pouvez reprendre l’apprentissage plusieurs jours après. Pour cela, il vous suffit de relancer l’algorithme d’optimisation avec les derniers paramètres internes trouvés et de continuer à les améliorer.
Les écueils de l’apprentissage
On l’oublie trop souvent, beaucoup de séquences d’apprentissage n’ont pas fonctionné ! Voici les différents écueils que vous pouvez rencontrer lors de la mise en place d’une méthode d’apprentissage :
La non convergence : une phase d’apprentissage peut ne pas converger ! En effet, il se peut que la courbe de l’erreur oscille fortement à chaque itération montrant que les poids trouvés sont associés à un apprentissage instable.
Un mauvais taux de réussite : votre apprentissage peut converger mais l’erreur peut rester haute traduisant des prédictions globalement mauvaises. Ne soyez pas impressionné par un pourcentage de bonnes réponses, ainsi un système qui prédit le sexe d’une personne avec un taux de réussite de 60% ne fait en fait que 10% de mieux qu’une réponse aléatoire avec une performance de base de 50%.
Le surapprentissage : si votre apprentissage conduit à un taux de bonnes prédictions de 99%, c’est un miracle ! Non pas forcément. En effet, il peut exister une sorte d’apprentissage par cœur, ainsi la fonction \(f\) est arrivée à identifier chaque échantillon en entrée pour fournir la réponse attendue. Pour détecter ce phénomène, on teste les performances sur des données jamais utilisées pendant la phase d’apprentissage. On parle des données de validation. Si un écart de performance apparaît entre la base d’apprentissage et la base de validation, on peut supposer qu’il y a eu surapprentissage.
L’évidence : dans des situations évidentes, l’apprentissage va chercher la conclusion la plus rapide ! Par exemple, pour classifier des images de grenouilles, de dauphins et de lions, très rapidement nous allons atteindre 100% de prédictions justes. Pour effectuer une bonne prédiction, dans ce contexte, il est inutile de déterminer la nature du sujet photographié. En effet, il suffit de se fier à la couleur moyenne de l’image pour classifier facilement ces trois catégories : une image plutôt verte correspondra à la catégorie grenouille, une image plutôt jaune à la catégorie lion et une image plutôt bleue à la catégorie dauphin.
Des ensembles déséquilibrés : si vous cherchez à classifier des images de chats et de chiens et que vous fournissez 1000 photos de chats et 10 photos de chiens, l’apprentissage va atteindre 99% de bonnes réponses très rapidement. Pour cela, il suffit de répondre toujours « chat » à la question, ce qui donne 99% de chance de réussir car vous avez une majorité de photos de chats dans votre base.
Note
Lorsque vous manquez d’échantillons pour votre apprentissage, une technique consiste à utiliser du data augmentation pour simuler des données supplémentaires. On peut par exemple créer des images à partir de légères translations et rotations des images d’origine.
Note
On peut aussi ajouter du bruit ou des tâches dans l’image d’origine. Cette technique permet de fournir des prédictions plus robustes aux perturbations, l’apprentissage ayant été effectué sur des données bruitées.
Exercices
Les paramètres à conserver en production
L’apprentissage comportent deux phases distinctes :
La phase d’apprentissage consistant, à partir d’une base de vérités terrains fixées, à faire évoluer les paramètres internes afin de minimiser l’erreur totale.
Une phase d’exploitation où les paramètres internes sont maintenant figés. Le système se comporte comme un expert auquel on présente de nouvelles informations pour connaître sa réponse.
Que doit-on conserver comme information une fois la phase d’apprentissage terminée ? Ces informations doivent être suffisantes pour traiter de nouvelles données (phase d’exploitation).
Les images contenues dans la base d’apprentissage |
|
La fonction \(f\) |
|
La fonction d’erreur |
|
Les réponses contenues dans la base |
|
La méthode d’optimisation |
|
Les paramètres internes de \(f\) |
Compréhension et mots-clefs
La fonction d’erreur peut donner des valeurs dans \(\mathbb{R}^3\).
Quel est le nom de la base de données contenant des images de chiffres ?
La fonction \(f\) donne toujours une seule valeur réelle.
Dans le processus d’apprentissage, la fonction d’erreur est optionnelle.
L’erreur totale correspond à la somme des erreurs depuis le début de l’apprentissage.
Différentes séquences d’apprentissage finissent toujours par converger vers des poids identiques.
Pour apprendre, la fonction \(f\) utilise des paramètres internes.
Le surapprentissage se produit lorsque l’apprentissage continue alors que l’erreur n’évolue plus.
L’apprentissage supervisé consiste à vérifier que l’erreur diminue tout au long du processus d’apprentissage.
La phase de validation consiste à présenter les données servant d’entraînement pour évaluer le taux de réussite.
Apprentissage d’une fonction binaire
Nous cherchons à apprendre la fonction booléenne \(EstPositif(x)\) valant \(0\) si \(x < 0\) ou \(1\) sinon. Pour cela, on utilise les échantillons ci-dessous qui vont servir de référence pour l’apprentissage :
\(x_i\) |
\(Res_i\) |
|---|---|
-5 |
0 |
0.5 |
1 |
Nous choisissons comme fonction d’apprentissage :
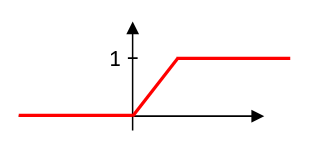
où \(x\) correspond à l’entrée et \(a\) au seul paramètre interne permettant l’apprentissage. Nous choisissons comme fonction d’erreur l’écart entre le résultat et la valeur de référence :
La prédiction \(f(-5,1)\) est-elle correcte ?
La prédiction \(f(0.5,1)\) est-elle correcte ?
Pour \(a=1\), calculez la valeur de l’erreur totale pour les échantillons donnés.
Pour \(a=1.2\), calculez la valeur de l’erreur totale pour les échantillons donnés.
En augmentant la valeur de \(a\) à la question précédente, l’erreur totale a-t-elle diminué ?`
Comme prochaine valeur de \(a\), vaut-il mieux tester \(1.4\) ou \(0.8\) ?
Pour \(a=4\), l’erreur totale est nulle. La fonction \(f(x,4)\) correspond-t-elle à la fonction \(EstPositif(x)\) ?
Comment apprendre ?
La fonction \(ErrTot()\) prend en entrée : une fonction \(f\), des paramètres internes \(w\) et une base d’apprentissage. Parmi ces trois entrées, les paramètres d’apprentissage \(w\) sont les seuls paramètres pouvant évoluer durant la phase d’apprentissage. Par conséquent, une fois la base et la fonction \(f\) choisies, le problème d’apprentissage se réécrit ainsi :
On reconnaît ici un problème d’optimisation classique : la recherche du minimum d’une fonction. Voici le code d’une méthode d’optimisation naïve qui fait évoluer les paramètres d’apprentissage \(w\) de manière à réduire l’erreur totale :
Function OptimNaif(ErrTot,f,w,DataSet) : ErreurMin = +∞ pas = 0.01 Tant qu’il reste du temps : # on génère aléatoirement des poids w’ dans le voisinage de w pour i allant de 0 à len(w) : w’[i] = w[i] + pas * random.uniform(-1,1) Erreur = ErrTot(f,w,DataSet) # si les nouveaux poids génèrent une erreur moindre, on les conserve Si Erreur < ErreurMin : w = w’ ErreurMin = ErreurDans la boucle principale cet algorithme, nous testons de nouveaux poids et calculons l’erreur totale associée. Si l’erreur totale s’avère plus faible, nous conservons ces nouveaux poids. Ainsi, en itérant, on arrive à diminuer l’erreur, l’apprentissage est opérationnel !