Descente du gradient + TD3

Nous avons vu que l’apprentissage requiert la minimisation d’une fonction d’erreur de \(\mathbb{R}^n\rightarrow \mathbb{R}\). Pour cela, une méthode très répandue existe : la méthode du gradient. Cette dernière permet itérativement de diminuer la valeur de l’erreur jusqu’à converger vers un minimum local. Dans ce chapitre, nous introduisons son principe, tout d’abord en traitant une fonction de \(\mathbb{R}\rightarrow \mathbb{R}\), puis ensuite une fonction de \(\mathbb{R}^2\rightarrow \mathbb{R}\) pour terminer en généralisant la méthode aux fonctions de \(\mathbb{R}^n\rightarrow \mathbb{R}\).

Pour une fonction de \(\mathbb{R}\rightarrow \mathbb{R}\)

Si nous traitons une fonction de \(\mathbb{R}\rightarrow \mathbb{R}\), dans ce cas particulier, la notion de gradient correspond à la notion de dérivée. Rappelons la formule d’approximation d’une fonction :

\[g(a+h) = g(a) + h \cdot g’(a) + \epsilon(h) ~ ~ ~ \mbox{ avec } ~ ~ ~ \lim_{h\rightarrow 0} \epsilon(h) = 0\]

Ce qui signifie qu’autour de la valeur \(a\), pour une valeur de \(h\) « petite », la fonction \(g\) se comporte comme une droite de pente \(g’(a)\) :

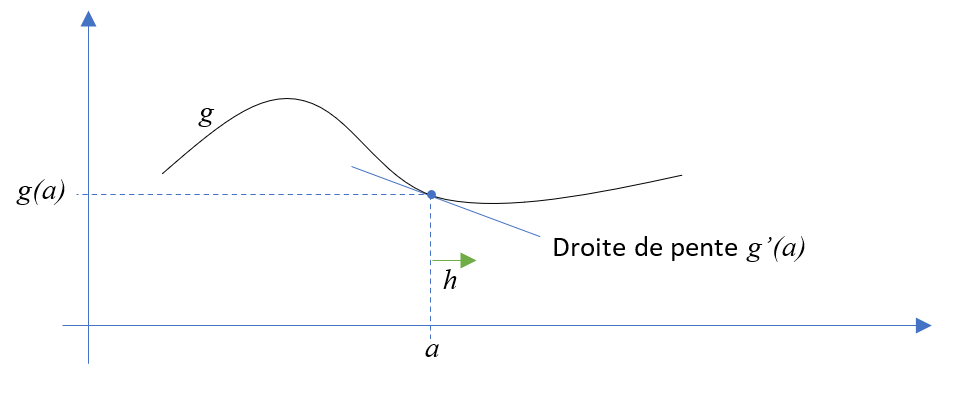
Considérons un processus itératif. Si l’on veut diminuer la valeur courante : \(g(a_i)\), il faut faire varier \(a_i\) dans le sens opposé au signe de \(g’(a_i)\). En effet, si la dérivée \(g'(a_i)\) est négative, la fonction \(g\) est décroissante au voisinage de \(a_i\). Par conséquent, lorsque \(g'(a_i)<0\), il faut augmenter la valeur de \(a_i\) : \(a_{i+1}>a_i\). De cette façon, en se déplaçant vers la droite, pour une variation suffisamment petite dénommée \(pas\), la valeur de \(g\) diminue. On en déduit la formule de principe de la méthode du gradient :

\[a_{i+1} = a_i - pas \cdot g’(a_i)\]

Nous utilisons cette approche pour mettre en place l’algorithme de descente du gradient :

Function GradientDescent(g,a) :
        pas = 0.01
        tant que du temps est disponible :
                grad = g’(a)        # dans notre exemple, la dérivée donne le gradient
                a = a – pas * grad  # le signe – fait progresser dans la direction opposée au signe de grad

Note

La méthode de descente du gradient ne garantit pas que la valeur de la fonction diminue à chaque itération. Par exemple, lorsque nous sommes proches d’un minimum, suivant la valeur du pas, on peut « sauter » par-dessus ce minimum pour atteindre finalement une valeur courante plus importante.

Avertissement

Dans la suite, une notation avec indice du type \(x_i\) désigne la valeur à l’itération \(i\). Ainsi, avec \(f(x)=3x^2+2\), si \(x_i=5\), nous pouvons évaluer la valeur de la fonction \(f'(x_i)\) égale à \(30\).

Exercice

Nous minimisions l’erreur totale d’une base contenant un unique échantillon \(x\) ceci en utilisant un seul paramètre interne \(a\) . Nous supposons que l’erreur totale est donnée par la fonction \(E(x,a) = a² + a\cdot x + 1\).

Donnée en entrée	\({x} = 3\)
Itération courante	\({a_i} = 5\)
Combien vaut \(E(3,{a_i})\) ?
Combien vaut \(\frac{\partial E}{\partial a}(3,{a_i})\) ?
Pour minimiser l’erreur, augmentons-nous la valeur de \({a_i}\) ?
Pour un pas de \(\frac{1}{13}\), donnez la nouvelle valeur de \({a_{i+1}}\)
Calculez \(E(3, a_{i+1})\) :
L’erreur a-t-elle diminué ?

Pour une fonction de \(\mathbb{R}^2\rightarrow \mathbb{R}\)

Pour minimiser une telle fonction, nous utilisons la notion de dérivée partielle qui étend la notion de dérivée d’une fonction de \(\mathbb{R}\rightarrow \mathbb{R}\) au cas général d’une fonction de \(\mathbb{R}^n\rightarrow \mathbb{R}\). Prenons l’exemple d’une fonction à deux variables \(g(x,y)\rightarrow \mathbb{R}\). En ajoutant un paramètre de perturbation \(h\), nous obtenons des formules d’approximation similaires au cas précédent :

\[g(x+h,y) = g(x,y) + h \cdot \frac{\partial g}{\partial x} (x,y) + \epsilon(h) ~ ~ ~ \mbox{ avec } ~ ~ ~ \lim_{h\rightarrow 0} \epsilon(h) = 0\]

et

\[g(x,y+h) = g(x,y) +h \cdot \frac{\partial g}{\partial y} (x,y) + \epsilon(h) ~ ~ ~ \mbox{ avec } ~ ~ ~ \lim_{h\rightarrow 0} \epsilon(h) = 0\]

Comment s’interprètent les deux dérivées partielles ? Si nous faisons uniquement évoluer la valeur de \(x\), nous obtenons comme dans le cas 1D une droite tangente au point courant \(P\). De la même manière, si nous faisons évoluer \(y\), nous obtenons une autre droite tangente en ce point. En combinant ces deux directions tangentes, nous obtenons un plan tangent qui approche le comportement de la fonction \(g\) autours du point \(P\) :

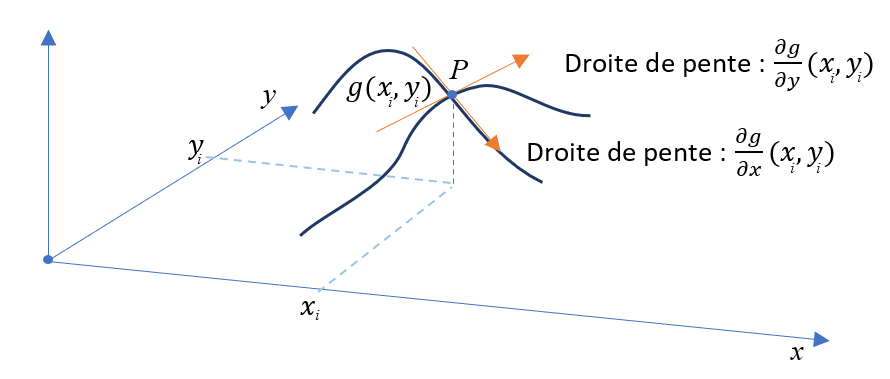
Nous utilisons la notation \(\nabla g\) pour désigner le gradient de la fonction \(g\). Ce vecteur correspond aux dérivées partielles de la fonction \(g\) :

\[\begin{split}\nabla g(x_i,y_i) = \begin{bmatrix} \frac{\partial g}{\partial x}(x_i,y_i) \\ \frac{\partial g}{\partial y}(x_i,y_i) \end{bmatrix}\end{split}\]

En utilisant des vecteurs, on peut regrouper les deux formules d’approximation précédentes en une seule. Ainsi, en prenant \(h=[h_0, h_1]\), \(X = [x, y]\) deux vecteurs colonnes, on peut écrire :

\[g(X+h)=g(X) + h^\top \cdot \nabla g(X) +\epsilon(h)\]

Pour minimiser la valeur de \(g\), on choisit \(h = -\gamma \cdot \nabla g(X)\) avec \(\gamma\) un réel positif suffisamment petit. En effet, ce choix implique :

\[g(X+h) \thicksim g(X) -\gamma [\nabla g(X)^\top \cdot \nabla g(X)]\]

Dans cette expression, la partie droite entre crochets correspond à un produit scalaire entre deux vecteurs identiques, ce qui donne comme résultat un nombre positif. La valeur de \(\gamma\) étant positive, l’expression à droite du signe - correspond ainsi à une valeur positive. En conclusion, la valeur de la fonction \(g\) va diminuer pour une valeur de \(\gamma\) suffisament petite.

Le cas général

Nous étudions maintenant le cas général avec une fonction \(g\) de \(\mathbb{R}^n\rightarrow \mathbb{R}\). Avec \(X\) et \(h\) désignant deux vecteurs de \(\mathbb{R}^n\), nous avons :

\[g(X+h) = g(X) + h^\top \cdot \nabla g(X) + \epsilon(h)\]

Comme dans le cas précédent, il suffit de prendre \(h=pas.\nabla g(X)\) avec \(pas>0\) suffisamment petit pour garantir que nous réduisons la valeur courante de la fonction. Ainsi, en appliquant cette formule itérativement, nous construisons l’algorithme de descente du gradient :

Function GradientDescent(g,X) :
        pas = 0.01  # valeur du pas
        tant que du temps est disponible :
                grad = ▽g(X)             # calcule les valeurs du gradient ▽g en X
                X    = X - pas . grad    # le signe – fait progresser dans la direction opposée au gradient

Note

Pour une fonction de \(g\) de \(\mathbb{R}^n\rightarrow \mathbb{R}\), le gradient \(\nabla g\) est un vecteur de taille \(n\) égale à la taille du vecteur \(X\). En effet, le gradient est un vecteur avec \(n\) composantes correspondant aux \(n\) dérivées partielles de \(g\). Par conséquent, on peut effectuer le calcul \(X - pas.\nabla g(X)\) car \(X\) et \(\nabla g(X)\) sont deux vecteurs de même dimension.

Note

Le paramètre \(pas\) est un réel positif, ainsi le signe . dans l’expression \(pas.\nabla g(X)\) désigne la multiplication entre un réel et un vecteur.

Exercice

Supposons que l’erreur totale s’écrive sous la forme : \(E(x,a,b) = a^2 + b\cdot x + 1\) avec

• \(x\) : donnée en entrée (constante).

• \(a,b\) : deux paramètres d’apprentissage.

Donnée en entrée	\({x} = 6\)
Valeur à l’itération courante	\(a_i = 3\), \(b_i = 2\)
Combien vaut \(E(6, {a_i}, {b_i})\) ?
Donnez les valeurs de \(\nabla E({a_i}, {b_i})\)
Pour un pas de \(\frac{1}{6}\), donnez les valeurs de \(a_{i+1}\) et \(b_{i+1}\)
Calculez \(E({6}, a_{i+1}, b_{i+1} )\) ?
L’erreur a-t-elle diminué ?

TD 3

Le source du Notebook

Vous devez effectuer ce TD et le faire valider à votre responsable de salle.