Broadcasting + TD2

Introduction

Pourquoi ne pas considérer que les tableaux NumPy se comportent comme des matrices ? Les matrices sont aussi des containers de données multidimensionnels similaires aux tableaux. On peut aussi ajouter deux tableaux NumPy comme on ajoute deux matrices. Mais les tableaux NumPy permettent des opérations non disponibles/non autorisés dans l’univers matriciel, comme par exemple ajouter un vecteur ligne à un vecteur colonne ! Ainsi, dans l’univers des tableaux Numpy, cette opération a un sens et elle s’appelle un broadcasting. Voici un exemple :

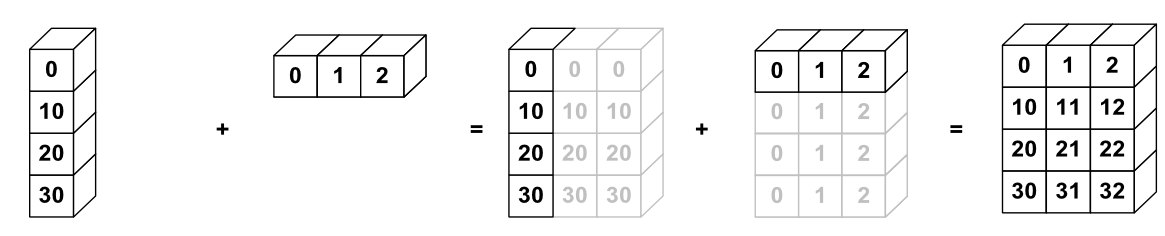
Que se passe-t-il ? Si vous ajoutez un tableau de taille \((4,1)\) avec un tableau de taille \((1,3)\), tout se comporte comme si chaque tableau était dupliqué autant de fois que nécessaire pour obtenir deux tableaux de taille \((4,3)\). Le résultat obtenu est ainsi un tableau de taille \((4,3)\). Voici un exemple :

import numpy as np

A = np.array([[0],[10],[20],[30]])
B = np.array([0,1,2])
A+B

>> array([ [ 0,  1,  2],
           [10, 11, 12],
           [20, 21, 22],
           [30, 31, 32] ])

Règle du broadcasting

Si intuitivement on comprend comment les opérations se déroulent, voici une manière plus rigoureuse de les expliquer. Notons \((a_0, \ldots, a_n)\) et \((b_0, \ldots, b_n)\) les dimensions des deux tableaux en entrée. Pour effecteur une opération de broadcasting entre deux tableaux, il faut vérifier si leurs dimensions sont compatibles :

\[\boxed{\mbox{Les dimensions des tableaux } A \mbox{ et } B \mbox{ sont compatibles si pour tout i, on a :} ~~~ ~ a_i=b_i ~~~\mbox{ou}~~~ a_i=1 ~~~\mbox{ou}~~~ b_i=1}\]

La taille \((s_0, \ldots, s_n)\) du tableau de sortie est donnée par la formule :

\[\boxed{s_i = \max(a_i,b_i)}\]

Taille des tableaux	Résultat
\((a_0,a_1) = (3,4)\) et \((b_0,b_1) = (3,2)\)
\((a_0,a_1) = (3,4)\) et \((b_0,b_1) = (1,4)\)
\((a_0,a_1) = (1,5)\) et \((b_0,b_1) = (3,1)\)

Aide :

Pour le premier indice, \(a_0 = b_0\) ce qui convient, mais \(a_1 \neq b_1\) et \(a_1, b_1 > 1\) donc les dimensions sont incompatibles.

Pour le premier indice, \(\ b_0=1\) ce qui convient et pour le deuxième indice : \(a_1 = b_1\) donc les dimensions sont compatibles et \(s = (3,4)\).

Pour le premier indice \(a_0 = 1\) et \(b_1= 1\), les dimensions sont compatibles et \(s = (3,5)\).

Dans le cas général, il est possible d’effectuer un broadcasting entre deux tableaux ayant un nombre différent de dimensions. On note \(a = (a_0, \ldots, a_n)\) et \(b = (b_0, \ldots, b_m)\) les dimensions des deux tableaux. Si \(n > m\), il suffit de considérer que le vecteur \(b\) a pour dimension :

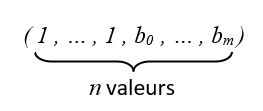
Cette transformation est peu coûteuse puisqu’elle équivaut à un reshape.

Représentation sous forme graphique

On peut trouver ce type de schéma en ligne :

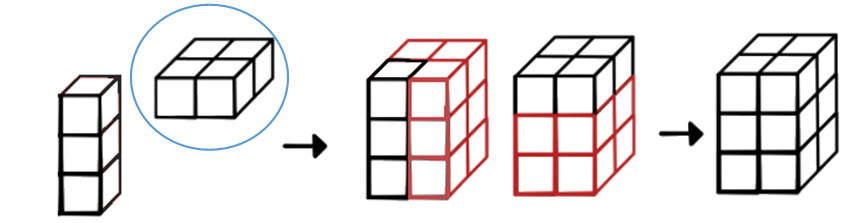
Le tableau 2D entouré en bleu est un tableau 2D de dimension \((2,2)\). Il est représenté couché en travers. Le vecteur colonne sur la gauche occupe une troisième dimension, il est donc de taille \((3,1,1)\). Ce qui donne après broadcasting un tableau de taille \((3,2,2)\).

\(a\)	\(b\)	\(s\)
\((3,4)\)	\((1)\)	\((3,4)\)
\((3,4)\)	\((1,1)\)
\((3,1)\)	\((4)\)
\((3,1)\)	\((1,4)\)
\((1,1,4)\)	\((1,3,1)\)
\((1,1,4)\)	\((3,2,1)\)

Tableau	Dimension
\([ 1, 2 ]\)	\((2)\)
\([ [1, 2] ]\)
\([ [1, 2], [3, 4], [5, 6] ]\)
\([ [[1]] ]\)
\([ [1], [1], [1]]\)
\([ [[1]], [[1]], [[1]] ]\)

Calculs

Pour construire le tableau C de dimension 2 par broadcasting deux tableaux A et B de dimensions compatibles, on applique la formule suivante :

\[C[i,j] = A[\lambda_A(i),\lambda_A(j)] + B[\lambda_B(i),\lambda_B(j)]\]

Avec \(\lambda_K(u)\) une fonction qui retourne l’indice \(u\) s’il est valide pour ce tableau \(K\) ou 0 sinon.

Exercice

[ [1, 2, 3], [4, 5, 6] ] + [ [0], [1] ]

A : [ [1], [2], [3], [5], [6], [7] ]

B : [ [1, 2, 3], [4, 5, 6], [2, 3, 4], [5, 6, 7] ]

C : [ [1, 2, 3], [5, 6, 7] ]

D : [ [[1, 2, 3], [4, 5, 6]], [[2, 3, 4], [5, 6, 7]] ]

Avertissement

Le système du broadcasting offre l’avantage d’une certaine souplesse. Cependant, son inconvénient est qu’il pourra masquer certaines de vos erreurs en produisant un résultat alors que les entrées sont de tailles non désirées. Par exemple, si vous pensiez ajouter deux images de même taille et que vous ajoutiez une image à un vecteur ligne, cela ne déclenchera pas forcément d’erreur si leurs dimensions sont compatibles par rapport au mécanisme du broadcasting.

TD2 Broadcasting

Le source du Notebook

Vous devez effectuer ce TD et le faire valider à votre responsable de salle.