Les fonctions d’erreur
Critère géométrique
MeanSquaredError
Cette fonction d’erreur calcule la moyenne des carrés des différences entre chaque valeur de référence et chaque valeur estimée par le réseau. Ainsi, la formule de calcul de la MSE pour deux vecteurs \(y_{true}\) et \(y_{pred}\) de \(n\) valeurs est égale à :
Par exemple, pour X=[6, 5, 1, 3, 5] et Y=[10, 2, 1, 4, 5], on obtient :
Ainsi la somme des carrés des éléments de X et Y est égale à 25. Comme il y a 5 éléments dans X et Y, nous obtenons au final une MSE de 5. Si les données en entrée ont plus d’une dimension, la MSE ignore ces dimensions et calcule la MSE des valeurs présentes. Ainsi, pour X = [ [1, 9], [2, 6], [9, 4] ] et Y = [ [4, 8], [12, 3], [10, 7] ], nous obtenons :
La somme des différences au carré est ainsi égale à 129. Comme 6 éléments sont présents, on obtient une MSE égale à \(\frac{1}{6} 129 = 21.5\).
Pour les valeurs suivantes, calculez l’erreur MSE associée:
Keras
La fonction d’erreur MSE est disponible dans Keras sous le nom MeanSquaredError() :
import tensorflow as tf
y_true = [0, 0, 1, 5]
y_pred = [10, 0, 1, 5]
mse = tf.keras.losses.MeanSquaredError()
mse(y_true, y_pred)
>> 25
Critère d’entropie : CrossEntropyLoss
Présentation
Nous introduisons une notion importante pour la suite : l’entropie permettant de caractériser le niveau de désorganisation ou d’imprédictibilité d’un système. Pour une distribution de probabilité discrète \(X(\Omega) = (x_i)_{0 \le i < n}\) associée aux probabilités \((p_i)_{0\le i < n}>0\), l’entropie est définie ainsi :
L’entropie est une grandeur positive : en effet, les probabilités étant des valeurs dans l’intervalle ]0,1], les termes en log sont tous négatifs. Ainsi le signe – avant le grand sigma donne un résultat positif.
L’entropie n’est pas une valeur bornée : en effet, si nous avons n valeurs équidistribuées, nous obtenons : \(H(X)=-\frac{n}{n}\cdot \ln(\frac{1}{n})\) ce qui donne \(H(X)= \ln(n)\).
L’entropie atteint son maximum lorsque les probabilités sont équidistribuées. Prenons le cas n=2, ainsi nous pouvons écrire : \(H(X) = -p\ln(p)-(1-p)\ln(1-p)\). En dérivant par rapport à p, nous obtenons \(H'=-\ln(p)+ln(1-p)\), dérivée qui s’annule pour \(p=\frac{1}{2}\).
Examinons un cas pratique avec trois boites contenant des billes rouges et des billes vertes :
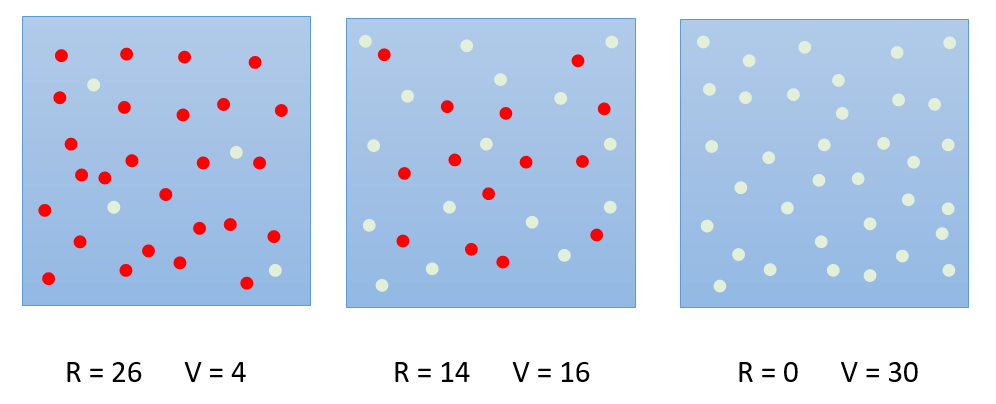
Dans la boite de gauche, la probabilité de tirer une boule rouge est de 26/30 et celle de tirer une bille verte est de 4/30. Ainsi, la probabilité de tirer une boule rouge est plus certaine.
Dans la boite au centre, la probabilité de tirer une boule rouge est de 14/30 et celle de tirer une bille verte de 16/30. Il y a presque une chance sur deux de tirer une boule rouge ou une boule verte. Il devient difficile d’être sûr de la couleur tirée.
Dans la boite de droite, nous sommes certains que la boule tirée sera de couleur verte. La probabilité de tirer une boule verte est de 1 contre 0 pour une boule rouge.
Calculons les valeurs de l’entropie pour chacune de ces situations :
Boite de gauche : \(-26/30\cdot ln(26/30) - 4/30\cdot ln(4/30) = 0.3926\)
Boite au centre : \(-14/30\cdot ln(14/30) - 16/30\cdot ln(16/30) = 0.6909 < ln(2)=0.6931\)
Boite de droite : \(-30/30\cdot ln(30/30) = 0\)
L’entropie de la boite de gauche est inférieure à la boite du centre car en tirant une boule dans cette boite nous sommes presque sûr qu’elle sera rouge. Dans la boite au centre, nous ne sommes sûr de rien, elle peut être rouge comme verte et l’entropie calculée est proche de l’entropie maximale possible : ln(2). La boite de droite correspond à une situation où nous sommes absolument certains que toute boule tirée sera verte, en conséquence l’entropie est nulle.
CrossEntropyLoss
Nous allons utiliser la définition de l’entropie croisée pour construire la fonction d’erreur Cross-Entropy Loss. L’entropie croisée pour deux distributions discrètes p et q est définie de la façon suivante :
Quand on compare une distribution de probabilités q avec une distribution de probabilités p, l’entropie croisée atteint son minimum lorsque les deux distributions sont égales i.e. \(p_i=q_i\) ce qui implique que l’entropie H(p) devient égale à l’entropie H(q).
Dans le processus d’apprentissage, les vérités terrain correspondent à une distribution de probabilités p connue. Le réseau doit lui chercher à construire la distribution de probabilités q afin qu’elle corresponde au mieux à la distribution de référence. Si nous calculons l’entropie croisée entre la distribution p (fixée) et q (estimée par le réseau) et que nous cherchons par le processus de descente du gradient à minimiser cette grandeur, alors cela équivaut à faire tendre la distribution q vers la distribution p.
Dans le problème de classification, lorsque nous savons que la catégorie donnée par le réseau doit correspondre à la catégorie icat, cela équivaut à dire que les probabilités obtenues en sortie du réseau devraient être toutes nulles à l’exception de la i-ème composante qui devrait être égale à 1 (100%). Ainsi, la distribution de probabilités p de référence correspond au vecteur suivant :
L’expression de l’erreur associée à l’entropie croisée se réécrit donc dans ce contexte :
\(CrossEntropyLoss(p_{icat},q) = - \ln{\left(q_{icat}\right)}\)
De l’expression précédente, il ne reste qu’un seul terme correspondant à la catégorie icat. Ainsi en minimisant la fonction CrossEntropyLoss, les poids du réseau s’optimisent pour que les probabilités en sortie de la fonction Softmax donnent une probabilité de 1 pour les catégories désirées.
Note
la fonction d’entropie croisée est souvent confondue avec la fonction logistic loss aussi appelée log loss. Bien que ces deux mesures soient des notions différentes, utilisées comme fonction d’erreur dans le problème de classification, elles calculent en fait la même grandeur et deviennent dans ce contexte équivalentes.
Comportement
La fonction d’erreur Cross-Entropy ou log loss, mesure la performance de prédiction du réseau. En effet, l’erreur est nulle lorsque la probabilité de la bonne catégorie atteint 100%. D’autre part, plus la probabilité s’éloigne de 1, plus l’erreur augmente. Voir l’exemple dans le graph ci-dessous :
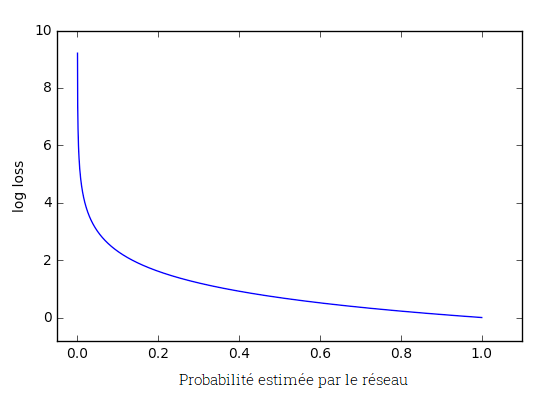
Lorsque la probabilité estimée s’approche de 1, la pénalité associée décroît lentement. Cependant, lorsque la probabilité estimée est inférieure à 20% et qu’elle continue à diminuer, alors la pénalité augmente très vite. Ainsi, cette fonction d’erreur est particulièrement sensible aux mauvaises prédictions car la valeur de l’erreur est très importante.
Keras
Différentes fonctions d’entropie croisée sont disponibles dans Keras et toutes calculent la même grandeur. Cependant, elles diffèrent par le format choisi pour représenter les vérités terrain :
Si les vérités terrain sont encodées sous la forme d’une série de 0 avec un seul 1 pour indiquer la classe correcte, on utilise la fonction d’erreur CategoricalCrossentropy. Exemple d’encodage pour un problème de classification avec 3 classes : [1,0,0] , [0,1,0], [0,0,1].
Si les vérités terrain sont encodées avec le numéro de la catégorie, on utilise la fonction d’erreur SparseCategoricalCrossentropy. Exemple d’encodage pour un problème de classification avec 3 classes : [0], [1] , [2].
Dans le cas où la sortie du réseau fournit une seule valeur, cette valeur, grâce à un threshold fixé par défaut à 0.5, traduit deux catégories. Le problème de classification ne peut alors traiter que deux classes. Les vérités terrains s’encodent sous la forme : 0 ou 1 et dans ce cas, on utilise la fonction BinaryCrossEntropy.
L’entropie d’une distribution de probabilités discrète est toujours positive.
L’entropie d’une distribution de probabilités discrète est une grandeur bornée.
L’entropie d’une distribution de probabilités discrète atteint son maximum avec des probabilités équiprobables.
Avec \(icat=0\) et \(q_0=\frac{1}{e}\) et \(q_1=1-q_0\), alors l’entropie croisée vaut \(1\).
L’erreur associée à l’entropie croisée est nulle lorsque les probabilités sont équiprobables.
Dans Keras, CategoricalCrossentropy s’utilise lorsque les catégories de référence sont données sous la forme d’un vecteur de zéros avec une valeur 1 indiquant la classe correcte.
Les métriques
Durant la phase d’apprentissage, les fonctions d’erreur permettent d’évaluer la qualité de la prédiction d’un réseau par rapport aux réponses exactes. Les fonctions de métrique, ou les métriques, ont un objectif similaire mais sont par contre utilisées uniquement durant la phase de validation du réseau. Ainsi, une fonction d’erreur peut être utilisée comme métrique alors qu’une métrique ne peut pas être utilisée comme fonction d’erreur. Pourquoi ? Simplement parce que les métriques ne sont pas adaptées à la méthode de descente du gradient. En effet, on peut citer l’exemple d’une métrique évaluant le pourcentage de réponses correctes, cette fonction est dérivable par morceaux mais sur chaque zone où elle est dérivable, sa dérivée est nulle, ce qui empêche l’algorithme de rétropropagation de fonctionner.
Pourcentage de prédictions réussies
Cette métrique évalue le pourcentage de bonnes prédictions. Cette métrique est intuitive et permet d’évaluer le taux de succés du réseau.
Logit
Il s’agit d’un terme ayant un sens spécifique dans le monde de l’apprentissage. Le logit désigne les valeurs brutes (non-normalisé) en sortie du réseau. Ainsi, dans les problèmes de classification, le logit est le vecteur de valeurs qui va ensuite être transmis à la fonction Softmax pour normalisation. Le logit est un vecteur de valeurs quelconques (non-normalisées) alors que le vecteur en sortie de la fonction Softmax est un vecteur de probabilités dont les valeurs sont dans l’intervalle [0,1] et dont la somme vaut 1.
Keras
Cette métrique existe dans Keras sous trois formes : SparseCategoricalAccuracy, CategoricalAccuracy et BinaryAccuracy :
SparseCategoricalAccuracy demande l’indice de la catégorie réelle comme référence.
CategoricalAccuracy demande un vecteur [ 0 0 0 1 0 0 0] (one_hot) comme référence.
BinaryAccuracy s’utilise lorsqu’une seule donnée est présente en sortie du réseau, le threshold (0.5 par défaut) fournissant la prédiction correspondante. Le vecteur des références contient des valeurs 0 ou 1.
Note
Les métriques SparseCategoricalAccuracy et CategoricalAccuracy prennent comme prédiction du réseau aussi bien des données sous forme de logit que sous forme de probabilités. En effet, la catégorie retenue dans les deux cas correspond à l’indice de la valeur maximale (argmax) du vecteur de prédiction.
Dans les deux exemples suivants, la première et la dernière prédiction s’avèrent correctes ce qui fait un ratio de 66% de bonnes réponses.
import tensorflow as tf
sparse = [[0], [1], [2]]
logits = [[.8, .1, .1], [.5, .3, .2], [.2, .2, .6]]
sparse_cat_acc = tf.metrics.SparseCategoricalAccuracy()
sparse_cat_acc(sparse, logits)
>> <tf.Tensor: shape=(), dtype=float32, numpy=0.6666667>
onehot = [[1., 0., 0.], [0., 1., 0.], [0., 0., 1.]]
logits = [[.8, .1, .1], [.5, .3, .2], [.2, .2, .6]]
cat_acc = tf.metrics.CategoricalAccuracy()
cat_acc(sparse, logits)
>> f.Tensor: shape=(), dtype=float32, numpy=0.6666667>
Les trois premières prédictions s’avèrent correctes ce qui fait un ratio de 75% de bonnes réponses :
y_true = [1, 1, 0, 0]
logit = [0.98, 1, 0.49, 0.51] # le threshold de binarisation est fixé par défaut à 0.5
m = tf.keras.metrics.BinaryAccuracy()
m( y_true, logit )
>> <tf.Tensor: shape=(), dtype=float32, numpy=0.75>
Une métrique peut être uniquement utilisée dans la phase de validation.
Une fonction d’erreur peut servir de métrique.
Un logit est le vecteur obtenu après un logloss.
Un logit est le codage en base 2 de la catégorie de l’échantillon.
La métrique CategoricalAccuracy s’applique uniquement sur des vecteurs de probabilités.
La métrique SparseCategoricalAccuracy prend comme entrée les numéro des catégories.
La métrique BinaryAccuracy prend comme entrée des valeurs quelconques.