Les optimiseurs
Nous avons présenté la méthode de descente du gradient (gradient descent) pour optimiser les paramètres internes du réseau afin de réduire l’erreur totale. Mais ce n’est pas la seule méthode, des améliorations et des variations de ces améliorations ont été mises en place pour accélerer et améliorer la convergence. Ainsi, ces différentes méthodes sont regroupées sous le terme d”optimiseurs (optimizers). Leurs noms sont donnés en anglais car elles apparaissent ainsi dans les librairies et dans le code source des programmes.
Les classiques
Gradient Descent
La descente du gradient utilise un pas fixe aussi appelé learning rate. Pour rappel, les paramètres du réseau évoluent en fonction du gradient de la fonction d’erreur :
Avantages :
Facile à comprendre.
Facile à programmer.
Inconvénient :
Nécessite d’évaluer l’erreur et son gradient sur l’ensemble des données en entrée. Lorsque le Dataset est important, cela ralentit considérablement chaque itération.
En pratique, la méthode de descente du gradient est peu utilisée telle quelle car elle requiert trop de temps. La variante suivante est la version plus commune.
Stochastic Gradient Descent (SGD)
Que signifie le terme stochastique ajouté au nom de la méthode du gradient ? Lorsque la taille des données en entrée devient importante, évaluer l’erreur totale et son gradient devient une opération très coûteuse. Nous rappelons de plus qu’au départ, les paramètres internes sont choisis aléatoirement et qu’il n’est donc pas utile d’avoir un gradient calculé de manière précise au vue de la piètre performance du réseau. Ainsi, pour améliorer la descente du gradient, on sélectionne aléatoirement un sous-ensemble des données en entrée pour estimer l’erreur et le gradient. Cette sélection étant faite aléatoirement à chaque itération, on qualifie le gradient de stochastique : fruit du hasard.
Avantages :
Les mises à jour sont plus fréquentes, c’est toujours bon pour le moral de voir le réseau évoluer régulièrement !
Dans la pratique, diminue le temps de convergence.
Inconvénients :
Du bruit apparaît dans le gradient et par conséquent dans la courbe de l’erreur aussi.
Lorsque l’on approche d’un optimum, la convergence est plus hasardeuse comparée à la méthode classique. On peut corriger cela en réduisant le learning rate.
Mini-Batch Gradient Descent
L’idée est la même que pour SGD, sauf qu’ici nous allons partitionner le Dataset des données en entrée en batchs de taille identique. Ainsi plutôt que de tirer au hasard les données à utiliser pour le calcul du gradient, on va itérativement traiter chaque minibatch. Ainsi, lorsque tous les batchs ont été traités, on dit que l’algorithme a terminé une epoch. L’apprentissage continue en repartant du premier batch dans la liste.
Lors de la création des batchs, il faut qu’ils soient générés aléatoirement ou équitablement. Ainsi pour un problème de classification, on ne peut pas faire un batch de chats puis un batch de chiens et ainsi de suite. Cela conduirait à une évaluation du gradient très biaisée. Il est donc recommandé d’avoir des batchs représentatifs avec une représentation équivalente de chaque classe. Ainsi, comparé à SGD, l’évaluation du gradient est moins bruité.
Momentum
On ajoute une technique à la méthode SGD pour réduire son bruit élevé. On accélère ainsi la convergence vers la direction pertinente et on réduit la fluctuation provenant des directions non pertinentes. Cette technique consiste à pondérer le gradient courant par la pondération des gradients précédents afin de lisser des changements de direction trop important. Pour cela, on utilise un nouvel hyperparamètre appelé le momentum symbolisé par \(\gamma\). Voici la formule utilisée :
Cette valeur \(V(t)\) est alors injectée dans la méthode de descente du gradient :
Par défaut, dans les librairies le momentum est fixé à 0.9.
Avantage :
Réduit le bruit et les oscillations présents dans SGD.
Désavantage :
Rajoute un hyperparamètre supplémentaire à gérer.
Adagrad
Dans la méthode de descente du gradient, vous remarquez que l’on utilise un pas constant ceci pour tous les paramètres internes. L’optimiseur Adagrad cherche à ralentir le pas des paramètres connaissant de fortes variations. Pour cela, l’optimiseur Adagrad introduit l’idée de mise à jour des paramètres internes avec un pas propre à chacun :
devient
L’indice i dans l’équation désigne le i-ème paramètre interne et l’indice t représente le numéro de l’itération. La grandeur SSG est la somme des gradients au carré pour le i-ème paramètre à partir de l’itération 0 jusqu’à l’itération t. La grandeur \(\epsilon\) est utilisée pour ajouter une petite valeur à SSG pour éviter une division par zéro. En divisant le pas par la racine carrée de SSG, on s’assure que le taux d’apprentissage pour les paramètres variant de manière importante diminue plus rapidement que les autres.
Avantages :
Le pas change et s’adapte pour chaque paramètre.
Cela supprime le besoin de régler/bidouiller le learning rate durant la convergence.
Désavantage :
Le learning rate de chaque paramètre ne fait que diminuer au fil du temps, ce qui ralentit la convergence.
Les optimiseurs avancés
Il existe d’autres optimiseurs plus avancés ayant pour objectif d’apporter une amélioration par rapport à un autre optimiseur. L’inconvénient est souvent l’apparition de multiples paramètres de réglage plus ou moins faciles à interpréter et à exploiter. La différence entre deux optimiseurs est parfois subtile, chacun étant une variation ou un mélange d’autres optimiseurs.
Dans l’approche Adagrad, on peut facilement remarquer que le dénominateur sous le terme pas a une valeur qui ne cesse d’augmenter au fil des itérations, car le terme \(\sqrt{SSG^t_i + \epsilon}\) ne fait que cumuler de plus en plus de valeurs positives au fil du temps et cela peut faire tendre le pas pondéré vers une valeur très faible.
RMSProp
Pour diminuer l’effet de ralenti se produisant au fil des itérations, la méthode RMSProp propose de pondérer le facteur d’amorti de l’itération précédente avec le carré du gradient courant pour construire le facteur d’amorti.
Cela a pour effet de redonner de l’importance aux valeurs du gradient courant et de diminuer l’influence des gradients trouvés lors des premières itérations.
Adadelta
Pour diminuer l’effet de ralenti se produisant au fil des itérations, Adadelta ne tient compte que des k derniers gradients pour calculer son facteur d’amortissement par paramètre.
Adam
Adam (Adaptive Moment Estimation) a repris les améliorations apportées par Adadelta et RMSProp en apportant une gestion des momentums au premier et au second ordre. Cet optimiseur est reconnu pour fournir de très bonnes performances et une vitesse de convergence accrue.
Quel optimiseur choisir ?
Les optimiseurs, c’est un peu comme les chevaux de course, il faut parier sur le bon ! Si vous êtes en mode recherche & développement, l’objectif est de trouver au moins un optimiseur qui converge. En cas de réussite, c’est une victoire.
Dans un deuxième temps, une fois que l’on sait résoudre le problème d’apprentissage avec un optimiseur, on peut tester d’autres variantes et d’autres hyperparamètres pour obtenir une convergence avec un temps optimal. C’est généralement le cas des optimiseurs que vous trouvez dans les exemples de code sur internet. L’optimiseur a été testé et comparé avec les autres optimiseurs et il s’est avéré fournir la meilleure convergence.
Pour un problème donné, le graphique ci-dessous présente les performances des différents optimiseurs :
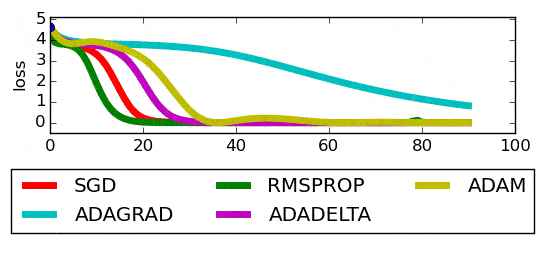
A partir de cette comparaison, il ne faut jamais conclure que tel ou tel optimiseur est le plus performant. La conclusion n’est valable que pour ce problème avec ces données. Cependant, certains optimiseurs sont connus pour se retrouver souvent dans le top 3.
Quel est l’intérêt de rechercher un optimiseur et des hyperparamètres fournissant une convergence optimale si un optimiseur a déjà fonctionné ? Les temps de convergence sont longs et se comptent en heures / jours / mois, gagner 20% ou 30% est donc important !
Quizzz
Adagrad, Adaf, SGD et Adam sont des optimiseurs.
Si l’on prend seulement les 100 premiers échantillons de la base pour estimer le gradient, le gradient est dit stochastique.
L’optimiseur Gradient Descent fonctionne mais il reste le plus lent.
Le Mini-Batch Gradient Descent consiste à choisir aléatoirement un lot d’échantillons pour évaluer le gradient.
L’optimiseur Adadelta est un des successeurs de l’optimiseur Adam.
Le paramètre de Momentum permet de lisser l’évaluation du gradient d’une itération à l’autre.
Le facteur de learning rate correspond au pas dans les méthodes de descente gradient.
La méthode Adagrad permet de moduler la converge de chaque paramètre du gradient.