Minimisation de l’erreur
Réseau séquentiel
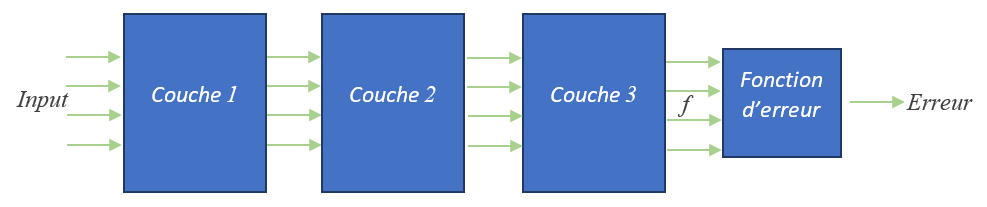
Les réseaux de neurones séquentiels, avec lesquels nous allons travailler, sont décrits sous forme de couches (layer). Chaque couche prend en entrée les informations en sortie de la couche précédente, puis effectue ses traitements pour transmettre ses résultats à la couche suivante. L’ensemble des couches constituent la fonction \(f\) correspondant à la prédiction de l’IA. Ensuite vient l’application de la fonction d’erreur qui permet d’obtenir comme résultat final un unique nombre réel correspondant à l’erreur.
Cette partie présente la méthode utilisée par les librairies d’apprentissage pour calculer le gradient d’un réseau y compris les plus complexes. Cette méthode, appelée rétro-propagation (Back Propagation), a été inventée par Yann le Cun et ses coauteurs ce qui leur valut le prix Turing en 2018. Aujourd’hui Yann le Cun est devenu directeur du centre de recherche en IA de Facebook appelé FAIR « Facebook Artificial Intelligence Research ». Pour la petite histoire, Yann le Cun est un ancien élève d’ESIEE Paris diplômé en 1983.
Avertissement
Nous utilisons une notation en majuscules pour désigner une variable correspondant à un vecteur.
Nous notons:
\(X_k\) le vecteur des entrées de la couche \(k\)
\(Y_k\) le vecteur des sorties de la couche \(k\), à noter que \(Y_k=X_{k+1}\).
\(W_k\) le vecteur des paramètres internes de la couche \(k\).
\(C_k()\) la fonction de traitement effectuée par la couche \(k\).
Nous rappelons ces notations dans le schéma suivant :
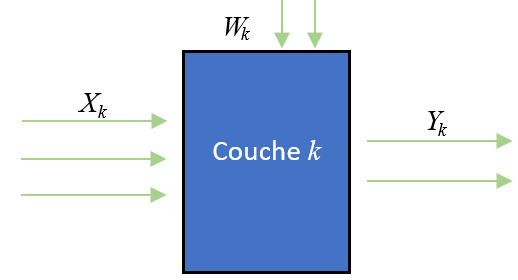
Ainsi nous avons :
La descente du gradient
Nous appliquons la méthode de descente du gradient au problème de la minimisation de l’erreur totale.
Gradient de l’erreur totale
Nous avons vu précédemment que l’erreur totale correspond à la sommation des erreurs induites par chaque échantillon :
Comme l’opérateur \(\nabla\) est linéaire, nous obtenons :
Ainsi, le gradient de l’erreur totale s’obtient en cumulant les valeurs des gradients associés à chaque échantillon. Nous obtenons donc l’algorithme de principe suivant pour la descente du gradient :
function Apprentissage() :
Tant qu'il reste du temps
Mise à 0 de ∇ErrTot(W)
# estimation de ∇ErrTot(W)
Pour chaque échantillon dans la base
Calculez ∇ErrEch(W) associé à cet échantillon
∇ErrTot(W) += ∇ErrEch(W)
# Minimisation de l'erreur / descente du gradient
W = W - pas * ∇ErrTot(W)
Calcul du gradient relativement à chaque couche
Pour appliquer l’algorithme de descente du gradient, il faut déterminer le gradient de l’erreur associée à un échantillon. Pour simplifier les écritures, dans la suite, on note \(E\) la fonction \(ErrEch\). Si nous avons \(m\) paramètres internes \(w_i\), nous cherchons à déterminer le gradient :
Pour des raisons pratiques, du à la topologie des réseaux séquentiels, nous n’allons pas déterminer successivement chaque valeur \(\frac{\partial E}{\partial w_i}\), au lieu de cela, nous allons traiter les paramètres internes par lot, en regroupant les paramètres d’une même couche. Nous notons \(W_k\) le vecteur des paramètres internes de la couche \(k\) :
Ainsi, le gradient de l’erreur associé à l’échantillon courant va être calculé par morceau, chaque morceau correspondant à une couche. Pour reconstruire le gradient, il suffit juste de concaténer les gradients issus de chaque couche. Par exemple, avec un réseau de \(3\) couches, on obtient :
Étape 1 : passe Forward
L’étape Forward consiste à faire transiter l’information de gauche à droite du réseau. Pour commencer, les valeurs d’un échantillon sont chargées dans le vecteur d’entrée. Ensuite, on calcule itérativement la sortie de la couche courante \(Y_i\), pour l’injecter en entrée de la couche suivante.
Une fois la sortie de la dernières couche calculée, on l’injecte dans la fonction d’erreur pour obtenir l’erreur associée à cet échantillon. La phase Forward est alors terminée. Les valeurs des vecteurs \(Y_i\) sont conservées en mémoire car elles vont être utilisées dans la phase suivante.
Voici le code de principe associé à la passe Forward :
Y[0] = Échantillon
pour i = 1 à nb_couches compris :
Y[i] = Couche_i(Y[i-1],W[i])
Erreur = FntErr(Y[nb_couches],reference_echantillon)
Étape 2 : passe Backward
Nous notons \(\overset{{Y_k}}{\nabla}E\) le gradient de la fonction \(E\) par rapport aux vecteurs de sortie \(Y_k\) de la couche \(k\). Ainsi, si \(Y_k=(y_0,\ldots,y_d)\), nous avons :
Dans la passe Backward, l’information va transiter de droite à gauche dans le réseau. Tout à droite du réseau, la fonction d’erreur est connue, il est donc facile de déterminer son gradient par rapport au vecteur \(Y_k\). Après cela, nous rétro-propageons (backpropgation) l’information \(\overset{{Y_k}}{\nabla} E\) à travers chaque couche. Pour cela, les librairies d’IA calcule pour chaque couche deux matrices de transfert \(M_1\) et \(M_2\) en utilisant les valeurs d’entrée de la couche courante soit \(Y_{k-1}\). Ces deux matrices permettent de calculer \(\overset{Y_{k-1}}{\nabla} E\) et \(\overset{W_{k}}{\nabla} E\) à partir de \(\overset{Y_k}{\nabla} E\) :
Voici le code de principe associé à la passe Backward :
n = nb_couches
GradY_E[n] = Grad(FntErr,Y[n])
pour i = n à 1 compris :
gradW_E[i] = M1⨯GradE[i]
gradY_E[i-1] = M2⨯GradE[i]
return (gradW_E[1],...,gradW_E[n])
Quiz
Quelle est la structure de l’algorithme de descente du gradient pour le problème d’apprentissage ?
\[\begin{split}\begin{aligned} A~~~~&\mbox{Boucle sur les échantillons}\\ &~~~~~~\mbox{Boucle d'optimisation}\\ &~~~~~~~~~~~~\mbox{Boucle sur les couches}\\ \\ B~~~~&\mbox{Boucle sur les échantillons}\\ &~~~~~~\mbox{Boucle sur les couches}\\ &~~~~~~~~~~~~\mbox{Boucle d'optimisation}\\ \\ C~~~~&\mbox{Boucle sur les couches}\\ &~~~~~~\mbox{Boucle d'optimisation}\\ &~~~~~~~~~~~~\mbox{Boucle sur les échantillons}\\ \\ D~~~~&\mbox{Boucle sur les couches}\\ &~~~~~~\mbox{Boucle sur les échantillons}\\ &~~~~~~~~~~~~\mbox{Boucle d'optimisation}\\ \\ E~~~~&\mbox{Boucle d'optimisation}\\ &~~~~~~\mbox{Boucle sur les échantillons}\\ &~~~~~~~~~~~~\mbox{Boucle sur les couches}\\ \\ F~~~~&\mbox{Boucle d'optimisation}\\ &~~~~~~\mbox{Boucle sur les couches}\\ &~~~~~~~~~~~~\mbox{Boucle sur les échantillons} \end{aligned}\end{split}\]Donnez votre réponse :
Pourquoi conserver les valeurs \(Y_i\) en mémoire ?
Pour calculer l’erreur totale.
Pour calculer les matrices de transfert lors de la rétro-propagation.
Pour calculer le gradient des échantillons suivants.
Donnez votre réponse :
Les valeurs des gradients associés au paramètres internes : \(\overset{\small{W_k}}{\nabla} ErrTot\) sont remises à zéro lorsque :
On traite l’échantillon suivant
On traite la couche suivante
On traite la prochaine itération de l’algorithme de descente de gradient
Donnez votre réponse :
Backpropagation
Nous présentons ici la rétro-propagation en détail. Cette partie est optionnelle et laissée au lecteur motivé.
Supposons que le réseau ait \(n\) couches, la fonction d’erreur prend donc comme entrée le vecteur \(Y_n\). Ainsi, nous obtenons le premier gradient qui va initier la rétro-propagation :
Supposons que \(Y_n=(y_0,y_1)\). Considérons la fonction d’erreur \(FntErr(y_0,y_1) = (y_0-ref)^2+(y_1-ref)^2\). Nous cherchons à déterminer l’expression de \(\overset{{Y_n}}{\nabla} E\) :
Cascadage
Supposons que le gradient \(\overset{\small{Y_k}}{\nabla} E\) ait été déterminé à l’itération précédente. A cette nouvelle itération, nous traitons la couche \(k\) et nous allons déterminer :
Le gradient \(\overset{\small{W_k}}{\nabla} E\) utilisé pour construire le gradient par rapport à tous les paramètres internes.
Le gradient \(\overset{\small{Y_{k-1}}}{\nabla} E\) utilisé pour propager le calcul du gradient vers la couche inférieure.
De cette façon, les itérations successives cascadent les informations des différents gradients \(\overset{\small{Y_k}}{\nabla} E\) de droite à gauche dans le réseau.
Traiter la couche courante
Nous traitons maintenant la k-ième couche. Pour alléger les notations, les vecteurs \(X_k\), \(Y_k\) et \(W_k\) sont notées : \(X\), \(Y\) et \(W\).
Regardons comment traiter la couche courante :
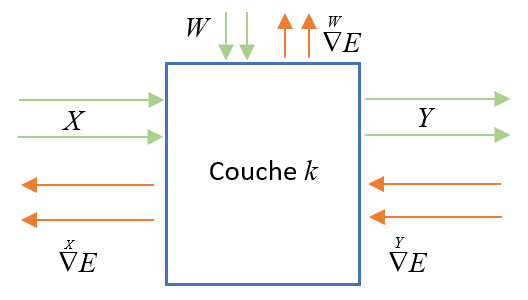
Le théorème général de dérivation énonce :
où \(J_{Y/X}\) désigne la matrice jacobienne de la fonction \(Y=C_k(X,W)\) par rapport aux variables \(x_0\), \(x_1, \ldots\) de \(X\).
De la même manière, ce théorème nous indique :
où \(J_{Y/W}\) désigne la matrice jacobienne de la fonction \(Y=C_k(X,W)\) par rapport aux variables \(w_0\), \(w_1, \ldots\) de \(W\).
Exemple
Nous utilisons un réseau de taille réduite composé d’une seule couche suivie d’une fonction d’erreur :
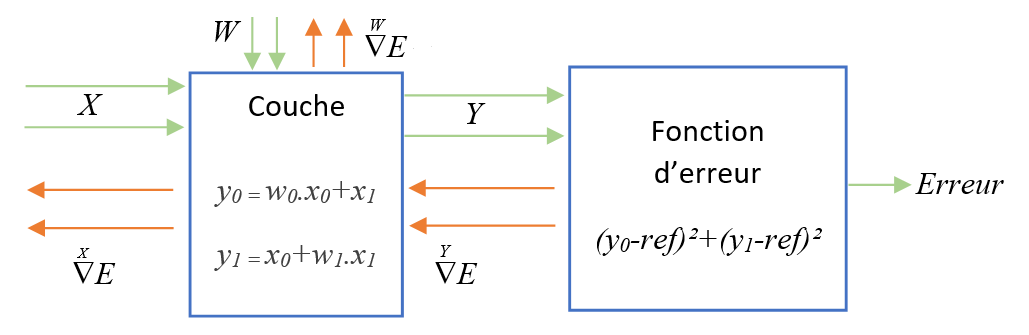
Nous calculons l’expression des deux matrices jacobiennes \(J_{Y/X}\) et \(J_{Y/W}\) :
et nous rappelons que :
Nous reprenons la notation de l’exemple ci-dessus.
Itération courante |
\({W}=(2,1)\), \({X}=(2,3)\) et \({ref}=4\) |
Calculez \({Y}\) |
|
Calculez \(FntErr(Y)\) |
|
Calculez \(\overset{{Y}}{\nabla} E({Y})\) |
|
Calculez \(\overset{{W}}{\nabla} E({X},{W})\) |
|
Calculez \(\overset{{X}}{\nabla} E({X},{W})\) |
|
Vérification
Comment vérifier nos résultats ? Il est possible d’évaluer la valeur d’une dérivée partielle en estimant la pente autours du voisinage courant. Voici le programme Python correspondant :
def g(x0,x1,w0,w1):
ref = 4
y0 = w0 * x0 + x1
y1 = x0 + w1 * x1
return (y0-ref)**2 + abs(y1-ref)**2
x0 = 2
x1 = 3
w0 = 2
w1 = 1
e = 0.001
v = g(x0,x1,w0,w1)
print(v)
# ∇g(W)
print( ( g(x0,x1,w0+e,w1) - v ) / e )
print( ( g(x0,x1,w0,w1+e) - v ) / e )
# ∇g(X)
print( ( g(x0+e,x1,w0,w1) - v ) / e )
print( ( g(x0,x1+e,w0,w1) - v ) / e )
Ce qui donne comme résultat :
>>> 10
>>> 12.003999999999238
>>> 6.009000000000597
>>> 14.00499999999738
>>> 8.00199999999407
Combien de matrices jacobiennes sont utilisées pour chaque couche ?
Donnez votre réponse :