Réseaux de neurones + TD4
Le neurone informatique
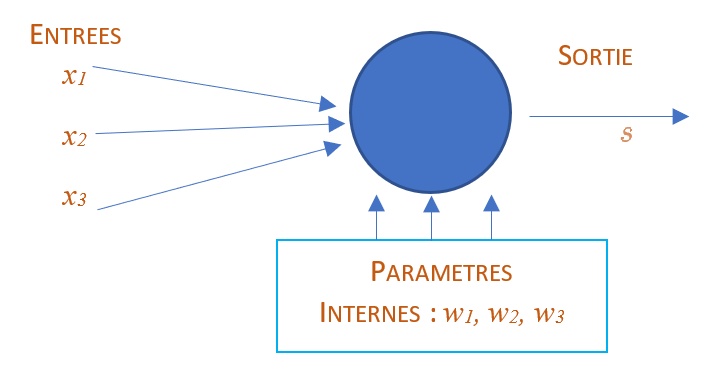
Un neurone dispose :
d’une UNIQUE sortie notée \(s\)
de \(n\) entrées notées \(x_i\)
de \(n\) paramètres internes notés \(w_i\)
éventuellement d’un paramètre interne supplémentaire appelé biais et noté \(b\)
Un neurone permet d’effectuer le calcul suivant :
A l’intérieur d’une même couche, on peut utiliser plusieurs neurones qui partagent les mêmes entrées. Ainsi, cette couche produit autant de valeurs de sortie que de neurones présents dans la couche. Voici le schéma correspondant :
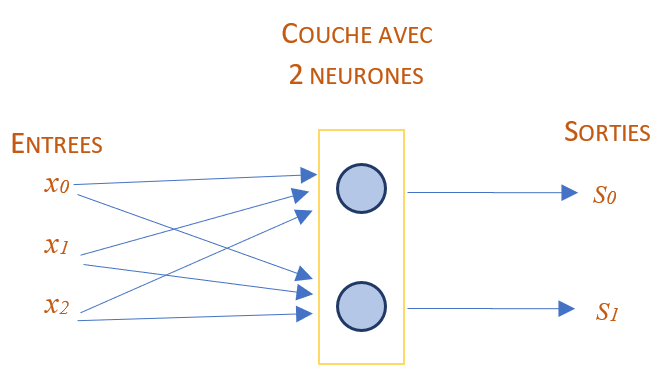
Ce type de couche est appelée Fully Connected (FC en agrégé) car chaque neurone de la couche en question est connecté à toutes les entrées. On trouve aussi le terme de couche Linear.
Lorsque nous avons \(n\) neurones et \(k\) valeurs d’entrée pour une couche donnée, cette couche a alors les caractéristiques suivantes :
La sortie de cette couche contient \(n\) valeurs
Cette couche contient \(n\) valeurs de biais \(b\) : une par neurone
Cette couche contient \(n(k+1)\) poids : \(n\) neurones avec \(k\) poids chacun plus le poids associé au biais.
Topologie des réseaux
Une couche Linear peut être représentée graphiquement à partir d’un rectangle vertical, contenant des ronds correspondant aux neurones.
Certains auteurs dessinent une couche d’entrée, « input layer » en anglais, même si cette couche ne contient aucun neurone. Cette couche « virtuelle » a pour fonction de « charger » les données, elle a donc un rôle « actif » ce qui explique sa présence dans certains schémas, même si, à proprement parler, elle n’effectue aucun calcul.
Les entrées sont généralement situées sur la gauche et les couches successives sont empilées de gauche à droite, la sortie finale du réseau se situe ainsi à l’extrémité droite :
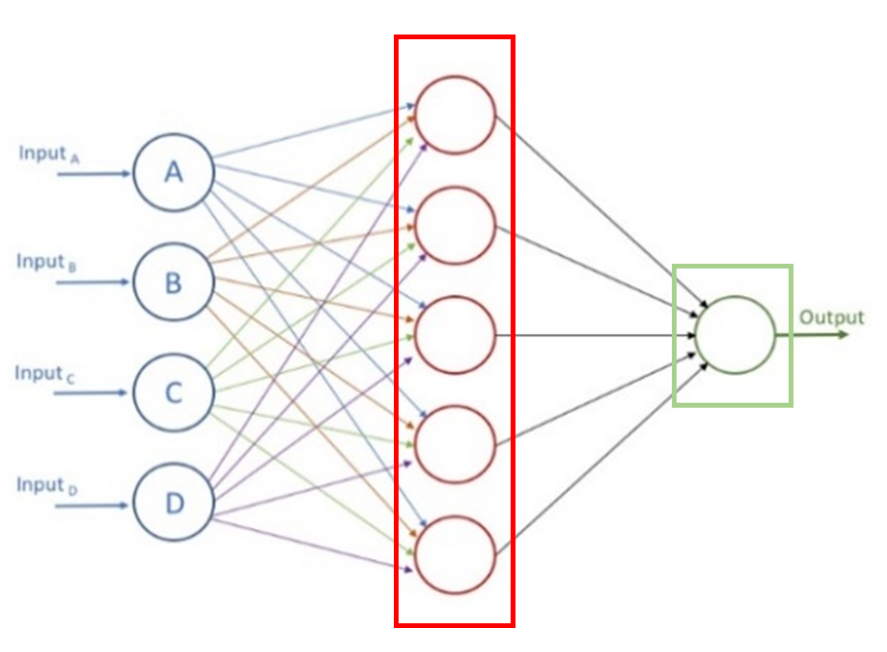
Schéma d’un « petit » réseau : une entrée avec quatre valeurs suivies d’une couche Linear au centre comportant 5 neurones et une deuxième couche Linear à droite ayant un seul neurone. Ce réseau donne une unique valeur de sortie.
On part du principe que les neurones présents dans le réseau ci-dessus disposent chacun d’une valeur de biais.
Combien ce réseau compte-t-il de poids ?
La fonction d’activation
Suffit-il d’empiler des couches pour construire un réseau ? Pas si sûr. En effet, prenons le cas de trois couches Linear sans biais. En l’absence de biais, chaque couche effectue l’équivalent d’une multiplication matricielle. Notons \(A_1\), \(A_2\) et \(A_3\) les matrices associées à chaque couche. Ainsi, la valeur de sortie du réseau peut être calculée de la manière suivante :
En prenant \(M=A_3 \cdot A_2 \cdot A_1\), l’équation ci-dessus se réécrit comme :
Ce qui permet d’affirmer que tout réseau à plusieurs couches est équivalent à un réseau à une seule couche. Ainsi, en empilant plusieurs couches Linear, on ne crée pas un réseau plus avancé qu’un réseau à une couche. Pour créer quelque-chose de nouveau, il faut donc ajouter entre chaque couche une « non-linéarité » et c’est ici le rôle des fonctions d’activation. Une fonction d’activation est une fonction de \(\mathbb{R}\rightarrow \mathbb{R}\) non-linéaire qui se connecte à la sortie de chaque neurone.
Généralement :
Dans une même couche, tous les neurones utilisent la même fonction d’activation.
Les fonctions d’activation n’ont pas de paramètres internes.
Une fonction assez populaire aujourd’hui est la fonction \(ReLU\) (Rectified Linear Unit) définie ainsi :
Dont le graph est :
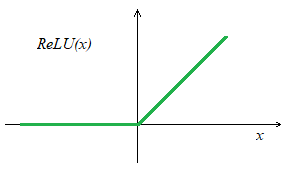
Il s’agit d’une fonction continue, dérivable quasiment partout et peu coûteuse en calcul ! Dans les schémas des réseaux de neurones, vous trouverez ainsi des commentaires sous chaque couche du type LINEAR+ReLU pour indiquer le type de couche utilisée ainsi que sa fonction d’activation. Avant que la fonction \(ReLU\) soit popularisée, on trouvait d’autres fonctions d’activation comme \(\tanh\) dont les valeurs de sortie sont entre -1 et 1 ou encore la fonction sigmoïde \(\sigma(x)\) dont les valeurs de sortie sont entre 0 et 1.
Réseau complexe
Il existe d’autres couches que les couches Linear. Elles effectuent des traitements différents mais le principe reste le même : elles prennent des données en entrée et fournissent des données en sortie. Ainsi, les réseaux complexes se construisent par empilage de plusieurs couches de natures différentes. Voici un exemple de réseau avec plusieurs couches traitant des images en entrée :
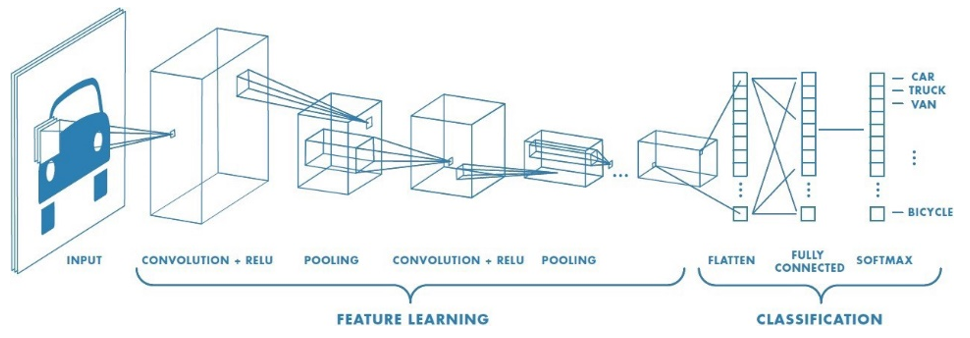
Dans ce schéma, on remarque que les couches ne sont pas dessinées, en effet, on préfère représenter les données produites par chaque couche sous la forme d’un rectangle ou d’un cube dont la taille symbolise la taille du tableau des données en sortie.
En dessous de chaque bloc est donné le nom de la couche correspondante. Ainsi dans ce schéma, on peut voir que l’on utilise successivement une couche Convolution puis une couche Pooling suivie d’une couche Convolution et d’une couche Flatten et enfin d’une dernière couche Fully Connected.
Chaque fois qu’une fonction d’activation est utilisée en sortie d’une couche, son type est précisé à côté du nom de la couche parfois avec un signe +. Ainsi dans ce réseau, les deux couches Convolution utilisent la fonction d’activation Relu et la dernière couche Fully Connected la fonction SoftMax.
En sortie du réseau on obtient plusieurs valeurs, chaque valeur étant associée à un type de véhicules (Car, Truck, Van, …, Bicycle). Il semble donc que ce réseau calcule pour une image en entrée une sorte de score / probabilité pour chaque type de véhicules.
Dans ce schéma, suffisamment d’informations sont données pour reproduire ce réseau. Cependant, il n’y a aucune information sur la fonction d’erreur qui a été utilisée lors de l’apprentissage.
Exercices
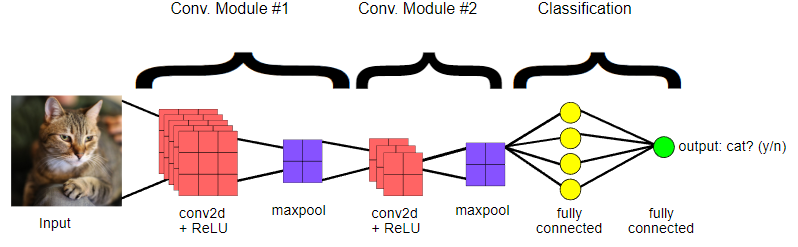
Question |
Réponse |
|---|---|
Combien de couches FC sont présentes dans le réseau |
|
Le nom de la fonction d’erreur est donné sur le schéma. |
|
Le nom d’une fonction d’activation est présent sur le schéma. |
|
Combien y-a-t-il de couches dans ce réseau ? |
|
Combien y-a-t-il de neurones dans la dernière couche ? |
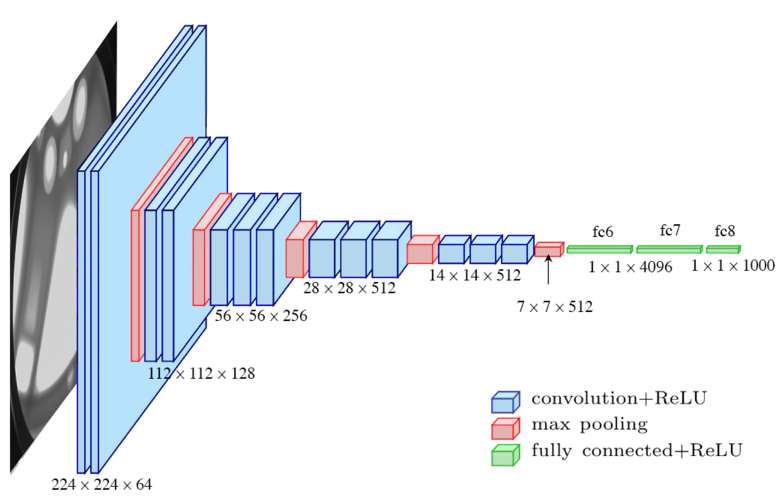
Question |
Réponse |
|---|---|
Le nom de la fonction d’erreur est donné sur le schéma. |
|
Combien y-a-t-il de couches FC dans ce réseau ? |
|
Combien y-a-t-il de couches de type Conv dans ce réseau ? |
|
Combien y-a-t-il de couches de type Max-Pooling dans ce réseau ? |
|
La fonction d’activation des couches FC est donnée sur le schéma. |
|
La fonction d’activation des couches Conv est donnée sur le schéma. |
|
La fonction d’activation des couches Max-Pooling est donnée sur le schéma. |
TD4
Vous devez effectuer ce TD et le faire valider à votre responsable de salle.