NumPy + TD1 + TD2
Vous pouvez tester en ligne les exemples grâce aux sites suivant :
NumPy permet d’exécuter des opérations complexes sur des tableaux en une seule instruction, évitant les boucles explicites et améliorant fortement les performances. Dans la suite, nous supposerons que nous avons importer la librairie NumPy ainsi :
import numpy as np
Les tableaux NumPy
Les tableaux NumPy sont des structures de données implémentées en C, stockant des valeurs de même type dans un bloc mémoire ce qui leur permet d’atteindre des performances proches du C. Ils servent de fondement à de nombreuses bibliothèques scientifiques comme PyTorch ou OpenCV.
Dans nos applications, nous devons stocker des données (images, sons, textes…). Par exemple, un lot de 50000 images de résolution 36x36 pourra être stocké dans un tableau de dimensions 50000x36x36.
Liens utiles :
Avertissement
Si vous ne précisez pas le type des éléments lors de la création d’un tableau, NumPy en choisit un suivant des règles implicites et il choisira très probablement un type 64 bits. En deep learning, pour éviter toute surconsommation mémoire et toute ambiguïté, il faudra explicitement donner le type voulu.
np.zeros(shape=(2,3), dtype=np.int32)
Crée un tableau 2x3 de valeurs entières nulles
np.ones(shape=(5,5), dtype=np.int32)
Crée un tableau 5x5 d’entiers valant 1
np.full(shape=(3,3), fill_value=4)
Crée un tableau 3x3 initialisé avec la valeur 4
np.arange(4)
Crée le NumPy array [0,1,2,3]
np.empty(shape=(3,2), dtype=np.float32)
Crée un tableau de flottants sans initialiser leurs valeurs
T.copy()
Duplique un NumPy array T
Fonctions de génération aléatoire :
np.random.randint(low=3, high=8, size=(2,4))
Tableau 2x4 avec valeurs aléatoires parmi 3, 4, 5, 6 et 7
np.random.rand(3,2)
Tableau 3x2 avec valeurs aléatoires dans [0,1[ avec distribution uniforme
np.random.normal(loc=0,scale=1,size=(3,2))
Tableau avec valeurs aléatoires suivant une loi normale(0,1)
Conversions
A = np.array(L)
Convertit une liste Python en NumPy array
L = A.tolist()
Convertit un NumPy array en liste Python
T2 = T1.astype(np.float32)
Crée un nouveau tableau dont les éléments correspondent au type indiqué
Dimensions
Indices & axes
Les tableaux NumPy peuvent être indexés :
Vecteur : T[i]
Matrice : T[i,j]
Volume : T[i,j,k]
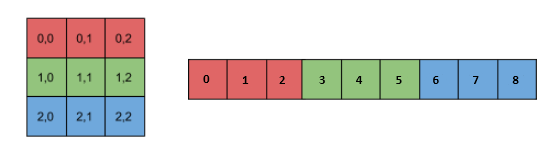
L’ordre de lecture des éléments d’un tableau suit le style du langage C : l’indice situé le plus à droite est celui qui varie le plus rapidement. Ainsi, l’élément qui suit T[0,0] est T[0,1], puis T[0,2], et ainsi de suite.
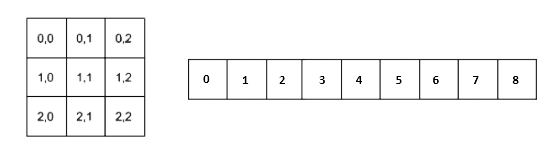
Il est possible d’indexer une dimension en partant de la fin, ainsi le dernier élément a pour indice -1, le suivant -2 et ainsi de suite :

Chaque dimension correspond à un axe. Par exemple, pour un tableau de dimensions (2, 4, 3), on obtient :
T[axe 0, axe 1, axe 2]
axe 0 : 2 indiçages - 0 et 1
axe 1 : 4 indiçages - 0, 1, 2 et 3
axe 2 : 3 indiçages - 0, 1 et 2
Sous-tableau
Si le nombre d’indices est inférieur au nombre de dimensions, alors l’indexation permet d’extraire un sous-tableau :
T = np.array( [[1,2,3],[4,5,6]] )
print(T[0]) >> [1,2,3]
print(T[1]) >> [4,5,6]
print(T[-2]) >> [1,2,3]
Avertissement
Rappelez-vous que l’indexation NumPy s’effectue avec des virgules : T[0,1,2]. Avec le mécanisme des sous-tableaux, il est possible d’obtenir le même résultat en écrivant T[0][1][2], mais cela revient à effectuer trois extractions successives, ce qui dégrade sensiblement les performances.
Changement de dimensions
Pour changer les dimensions d’un tableau, les nouvelles dimensions doivent contenir le même nombre d’éléments.
T.resize((3,2))
Modifie les dimensions du tableau T (in-place)
T2 = T1.reshape((3,2))
Renvoie un nouveau tableau avec les dimensions demandées, version non in-place
T.shape
Retourne les dimensions du tableau T
T.size
Retourne le nombre d’éléments dans le tableau T
T.ndim
Retourne le nombre de dimensions du tableau T
T.dtype
Retourne le type des données de T
Par conséquent, les éléments d’un tableau réorganisé conservent le même ordre en mémoire que le tableau original.
Quelle fonction crée un tableau initialisé avec des 1 ?
Quelle fonction crée un tableau initialisé avec des 0 ?
Quel argument permet de sélectionner le type des données ?
Quel package fournit la fonction rand() ?
Quelle fonction crée un tableau NumPy depuis une liste Python ?
Quelle fonction convertit les éléments d’un tableau vers un autre type ?
Quelle fonction change les dimensions d’un tableau en mode inplace ?
Quelle propriété n’appartient pas à un tableau Numpy : dim ou shape ?
Quelle propriété retourne le type des données : type, dtype, ntype, xtype ?
Pour un tableau de dimensions (3,4,5), l’axe 2 a quelle taille ?
Quelle est langage fonction qui transforme une liste en tableau ?
Peut-on effectuer un reshape((2,3)) sur un tableau A = np.arange(4) ?
Pour un vecteur de taille 5, l’écriture T[2] et T[-3] est-elle équivalente ?
Vue
Pour pouvoir travailler efficacement sur de grands tableaux sans multiplier les copies en mémoire, NumPy a introduit le mécanisme des vues. Ainsi, l’appel d’une fonction Numpy peut, ce n’est pas systèmatique, retourner un tableau qui ne possède pas ses propres données mais qui les partage avec le tableau d’origine. Par exemple, ce choix est judicieux pour la fonction reshape.
Cependant, il faut savoir que toute modification du tableau-vue va modifier le tableau original :
x = np.arange(4) >> array([0, 1, 2, 3])
y = x.reshape((2,2)) >> array([[0, 1],[2, 3]])
y[0,0] = 9
x >> array([9, 1, 2, 3])
y >> array([[9, 1],[2, 3]])
Il faut connaître cette réalité pour éviter certaines surprises. Si vous voulez rompre explicitement le possible lien vers un tableau, il faut utiliser la fonction copy(). En deep-learning, les tenseurs des librairies d’IA comme Pytorch ou TensorFlow ont repris la logique des vues car dans un GPU le souci d’optimisation mémoire est encore plus présent.
La fonction reshape peut retourner une vue.
La fonction reshape crée toujours une copie.
Les vues permettent d’optimiser l’utilisation de la mémoire.
Le mécanisme des vues n’existe par dans PyTorch et Tensorflow.
Le paramètre axis
La fonction mean() des tableaux Numpy calcule la moyenne des valeurs du tableau. Cependant, grâce à l’argument axis, on peut effectuer le calcul dans une direction donnée, ce qui est très intéressant :
Pour un tableau T de dimension (2,4,3), si on écrit T.mean(axis=2), NumPy va retirer cette dimension du résultat en effectuant la moyenne sur cet axe :
T.means(axis=0) => shape = (4,3)
T.means(axis=1) => shape = (2,3)
T.means(axis=2) => shape = (2,4)
Pour un tableau T de dimension (2,4,3,6,5) si on donne plusieurs directions, on continue à appliquer la même logique :
T.means(axis=(1,2)) => shape = (2,6,5)
T.means(axis=(0,4)) => shape = (4,3,6)
Voici une interprétation graphique :
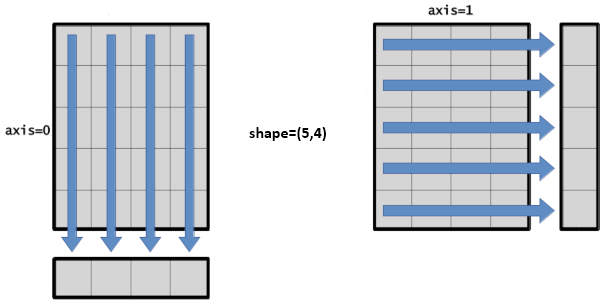
Le paramètre axis est utilisé par de nombreuses autres fonctions comme sum, max, min, std, var…
A noter qu’il existe un paramètre supplémentaire keepdims=True, qui permet d’obtenir un tableau avec autant de dimensions que le premier. Ainsi avec un tableau T de dimension (2,4,3,6,5) on obtient :
T.means(axis=(0,4),keepdims=True) => shape = (1,4,3,6,1)
Pour un tableau T = np.array([[1,2,3,4],[5,6,7,8]]), que retourne : T.max(axis=1) ?
réponse A: [5 6 7 8] ou réponse B: [4 8]
Pour un tableau T = np.array([[0,1,2],[3,4,5],[6,7,8]]), que faut-il écrire pour obtenir : [2 5 8] ?
réponse A: T.max(axis=0) ou réponse B: T.max(axis=1)
Pour T = np.array([ [[11,12],[13,14]], [[21,22],[23,24]], [[31,32],[33,34]] ]), que faut-il écrire pour obtenir [ [13,14], [23,24], [33,34] ] comme réponse ?
réponse A: T.max(axis=0) ou réponse B: T.max(axis=1) ou réponse C: T.max(axis=2)
Que faut-il écrire pour obtenir [33, 34] comme réponse avec le même tableau T ?
réponse A: T.max(axis=(0,1)) ou réponse B: T.max(axis=(1,2)) ou réponse C: T.max(axis=(0,2))
Plage d’indices - slicing
Il est possible d’utiliser la syntaxe start:stop ou start:stop:step pour représenter une plage d’indices. Ce mécanisme, appelé slicing, permet d’éviter l’utilisation de boucles et facilite la lecture du code.
T[0:5] |
Indices de 0 à 4 |
T[0:8:2] |
Indices : 0, 2, 4, 6 |
A[:5] |
Jusqu’à l’indice 4 compris |
A[5:] |
De l’indice 5 jusqu’à la fin |
A[:] |
Tous les indices |
Avec des tableaux 2 dimensions :
A = np.array( [ [10,11,12,13],
[20,21,22,23],
[30,31,32,33],
[40,41,42,43] ] )
A[1:3,1:3] # sélection des A[i,j] avec 1≤i<3 et 1≤j<3
>> array([[21, 22],
[31, 32]])
A[1:3,1:3] = 99 # affectation des indices sélectionnées
>> array([ [10, 11, 12, 13],
[20, 99, 99, 23],
[30, 99, 99, 33],
[40, 41, 42, 43]])
Ou encore :
A = np.array([ [1,2,3,4],
[6,7,8,9] ])
A[:,:2] # toutes les lignes, tous les indices < 2
>> array([[1, 2], [6, 7]])
Ou encore :
A = np.array( [ [10,11,12,13,14,15],
[20,21,22,23,24,25],
[30,31,32,33,34,35],
[40,41,42,43,44,45] ] )
A[:, 0:6:2 ] = 99 # affection des colonnes 0 2 4
==> array ([ [99, 11, 99, 13, 99, 15],
[99, 21, 99, 23, 99, 25],
[99, 31, 99, 33, 99, 35],
[99, 41, 99, 43, 99, 45]])
Ou encore :
A = np.array([ [1,2,3,4],
[6,7,8,9] ])
A[1] # 2eme ligne
A[1,:] # idem
>> array([6, 7, 8, 9])
A[0,2:] # 1ere ligne, tous les indices >=2
>> array([3, 4])
A[1,:2] # 2ème ligne, tous les indices < 2
>> array([6, 7])
Indexage avancé
Par listes d’index
Cette technique se déclenche lorsque l’indexation se fait à partir de listes. Elle permet de sélectionner les éléments \((x_i,y_i)\) d’un tableau en transmettant les deux listes \((x_i)\) et \((y_i)\) :
A = np.array( [ [10,11,12,13,14,15],
[20,21,22,23,24,25],
[30,31,32,33,34,35],
[40,41,42,43,44,45] ] )
A[[0,0,3,3],[0,5,0,5]] # extrait les valeurs aux positions [0,0], [0,5], [3,0] et [3,5]
>> array([10, 15, 40, 45])
A[[0,0,3,3],[0,5,0,5]] = 99 # affecte les valeurs aux positions [0,0], [0,5], [3,0] et [3,5]
>> [[99 11 12 13 14 99]
[20 21 22 23 24 25]
[30 31 32 33 34 35]
[99 41 42 43 44 99]]
On peut coupler la technique d’indexage avancé avec d’autres :
A = np.array( [ [10,11,12,13,14,15],
[20,21,22,23,24,25],
[30,31,32,33,34,35],
[40,41,42,43,44,45] ] )
A[[1,2],:] # extrait la 2ème et la 3ème ligne du tableau
>>array([[20, 21, 22, 23, 24, 25],
[30, 31, 32, 33, 34, 35]])
A[:,[1,2]] # extrait la 2ème et la 3ème colonne du tableau
array([[11, 12],
[21, 22],
[31, 32],
[41, 42]])
Par booléens
Un tableau A peut être indexé à l’aide d’un masque correspondant à un tableau de booléens. Le masque doit être de même dimension que le tableau A, il sert ainsi à indiquer quels éléments sélectionner (True) et lesquels ignorer (False). La syntaxe A[mask] extrait Les éléments sélectionnés vers un vecteur 1D :
A = np.arange(12).reshape(3,4)
mask = A > 5
vector = A[mask]
----- A -----
[[ 0 1 2 3]
[ 4 5 6 7]
[ 8 9 10 11]]
----- mask -----
[[False False False False]
[False False True True]
[ True True True True]]
----- vector -----
[ 6 7 8 9 10 11]
La syntaxe A[mask] = … applique l’affectation uniquement sur les éléments sélectionnés. On peut par exemple écrire :
A[A>4] = 0
----- A -----
[[ 0 1 2 3]
[ 4 0 0 0]
[ 0 0 0 0]]
Pour A = np.array([ [0,1],[2,3],[4,5]]), écrivez sous la forme x,y l’indexation de A retournant la valeur 2 .
Pour A = np.array([[[0,1],[2,3],[4,5]]]), donnez l’indexation de A retournant la valeur 5 (indices positifs).
Pour un tableau 1D, si A[-3] désigne la même cellule que A[3], quelle est la taille de ce tableau ?
Pour le tableau A : [[0,1,2],[4,5,6],[7,8,9]], quels sont les chiffres extraits par : A[[0,2,0,2],[0,0,2,2]]. Donnez les chiffres séparés par des espaces.
Broadcasting
Introduction
Pourquoi ne pas simplement considérer les tableaux NumPy comme des matrices ? Parce qu’ils permettent des opérations qui seraient interdites dans le monde strictement matriciel comme par exemple : additionner un vecteur ligne à un vecteur colonne ! En NumPy, cette liberté porte un nom : le broadcasting. En voici un exemple :
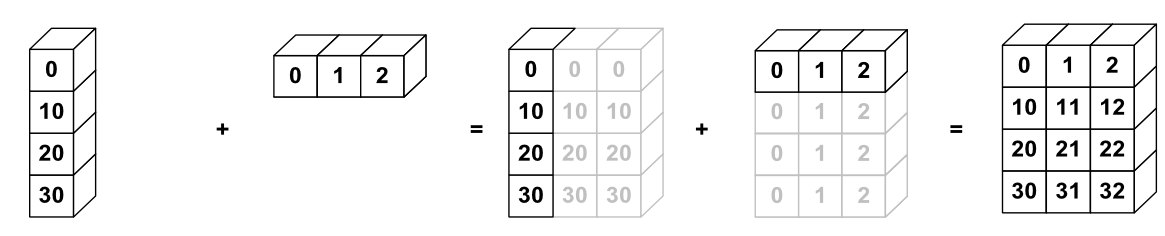
Que se passe-t-il ? Si vous ajoutez un tableau de taille \((4,1)\) avec un tableau de taille \((1,3)\), tout se comporte comme si chaque tableau était dupliqué autant de fois que nécessaire pour obtenir deux tableaux de taille \((4,3)\). Le résultat obtenu est ainsi un tableau de taille \((4,3)\). Voici un exemple :
import numpy as np
A = np.array([[0],[10],[20],[30]])
B = np.array([0,1,2])
A+B
>> array([ [ 0, 1, 2],
[10, 11, 12],
[20, 21, 22],
[30, 31, 32] ])
Règle du broadcasting
Notons \((a_0, \ldots, a_n)\) et \((b_0, \ldots, b_n)\) les dimensions des deux tableaux en entrée. Pour effecteur une opération de broadcasting entre ces deux tableaux, il faut vérifier que chaque dimension \(a_i\) soit compatible avec \(b_i\) :
Les dimensions \(a_i\) et \(b_i\) sont compatibles si : \(a_i = b_i\) ou \(a_i = 1\) ou \(b_i = 1\)
La taille \((s_0, \ldots, s_n)\) du tableau de sortie est donnée par la formule :
Taille des tableaux |
Résultat |
|---|---|
(3,4) et (3,2) |
|
(3,4) et (1,4) |
|
(1,5) et (3,1) |
Aide :
Pour le premier indice, \(a_0 = b_0\) ce qui convient, mais \(a_1 \neq b_1\) et \(a_1, b_1 > 1\) donc les dimensions sont incompatibles.
Pour le premier indice, \(\ b_0=1\) ce qui convient et pour le deuxième indice : \(a_1 = b_1\) donc les dimensions sont compatibles et \(s = (3,4)\).
Pour le premier indice \(a_0 = 1\) et \(b_1= 1\), les dimensions sont compatibles et \(s = (3,5)\).
Cas général
Notons \(a = (a_0, \ldots, a_n)\) et \(b = (b_0, \ldots, b_m)\) les dimensions des deux tableaux A et B. Pour effectuer un broadcasting entre A et B avec \(n > m\), il suffit de procéder comme auparavant en considérant que le tableau B a pour dimensions :
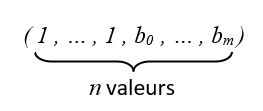
Exemple :
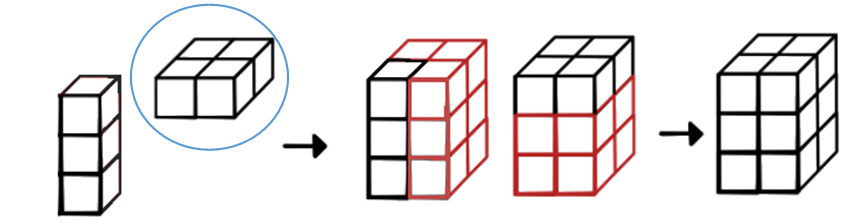
Le tableau entouré en bleu est un tableau de dimensions \((2,2)\), le vecteur colonne sur la gauche a pour dimensions \((3,1,1)\). Après broadcasting, le résultat est un tableau de taille \((3,2,2)\).
\(a\) |
\(b\) |
\(s\) |
|---|---|---|
\((3,4)\) |
\((1)\) |
\((3,4)\) |
\((3,4)\) |
\((1,1)\) |
|
\((3,1)\) |
\((4)\) |
|
\((3,1)\) |
\((1,4)\) |
|
\((1,1,4)\) |
\((1,3,1)\) |
|
\((1,1,4)\) |
\((3,2,1)\) |
Tableau |
Dimension |
|---|---|
\([ 1, 2 ]\) |
\((2)\) |
\([ [1, 2] ]\) |
|
\([ [1, 2], [3, 4], [5, 6] ]\) |
|
\([ [[1]] ]\) |
|
\([ [1], [1], [1]]\) |
|
\([ [[1]], [[1]], [[1]] ]\) |
Calculs
Pour construire le tableau C de dimension 2 par broadcasting deux tableaux A et B de dimensions compatibles, on applique la formule suivante :
La notation \(\overline{i}\) correspond à l’indice \(i\) s’il est valide ou à l’indice 0 sinon.
Exercice
[ [1, 2, 3], [4, 5, 6] ] + [ [0], [1] ]
A : [ [1], [2], [3], [5], [6], [7] ]
B : [ [1, 2, 3], [4, 5, 6], [2, 3, 4], [5, 6, 7] ]
C : [ [1, 2, 3], [5, 6, 7] ]
D : [ [[1, 2, 3], [4, 5, 6]], [[2, 3, 4], [5, 6, 7]] ]
Avertissement
Le système du broadcasting offre l’avantage d’une certaine souplesse. Cependant, son inconvénient est qu’il pourra masquer certaines de vos erreurs en produisant un résultat alors que les entrées sont de tailles non désirées.
Pour finir
Quelques fonctions utiles que vous rencontrerez sûrement dans des exemples :
T.ravel() : variante de reshape qui retourne un tableau 1D contenant tous les éléments de T : aplatissement
T.flatten() : comme ravel, mais renvoie toujours une copie
T.transpose() : retourne le tableau nD transposé
T.argmin() : retourne l’indice de la plus petite valeur dans un tableau, la première rencontrée s’il y en a plusieurs
T.swapaxes(…) : échange deux axes d’un tableau NumPy (sans copier les données)
np.expand_dims(T,…) : ajoute un axe supplémentaire
T.squeeze() : retire les dimensions de taille 1
concatenate / stack / hstack / vstack : utiles pour fusionner des tableaux
TD1 Numpy Array
Vous devez effectuer ce TD et le faire valider à votre responsable de salle.
TD2 Slicing and images
Vous devez effectuer ce TD et le faire valider à votre responsable de salle.