Overview#
The goal of this project is to develop a retrieval system that can search for images based on a predefined set of visual attributes. The system works by:
computing the similarity score between a query attribute vector and each image in the retrieval dataset,
ranking the images based on their similarity score,
returning the top-ranked images as the most relevant results.
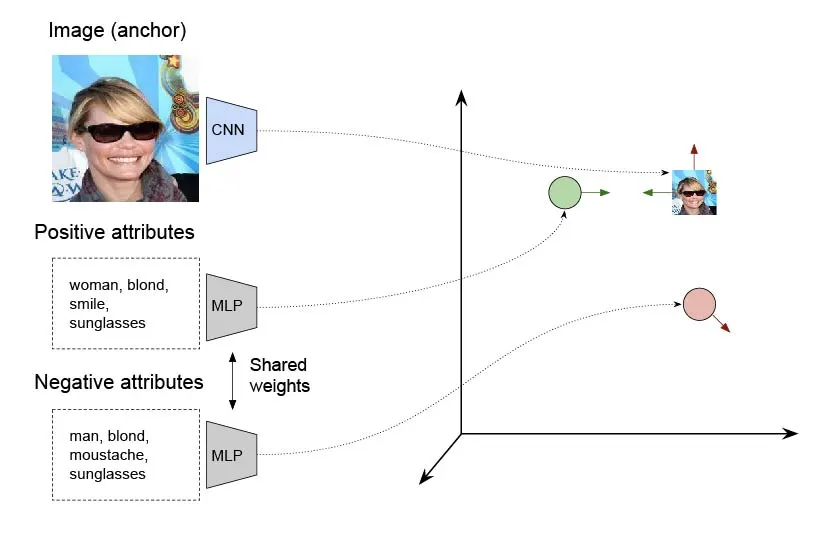
You will implement the retrieval system using deep metric learning in a multimodal setting, where embeddings are learned from two distinct data types: images and attributes. A convolutional network (CNN) will generate embeddings from images, while a fully-connected network (MLP) will generate embeddings from attributes. Despite processing different types of data, both networks are designed to produce outputs in the same embedding space, allowing for direct comparison between images and attributes.
Loss function#
Ideally, the embeddings of an image should be close to the embeddings of its correct attribute vector, while being far from the embeddings of incorrect attribute vectors. To accomplish this, you will train the networks using a triplet loss function that takes the following inputs:
Anchor: The embedding of an image.
Positive: The embedding of the attribute vector associated with the anchor image.
Negative: The embedding of an attribute vector that does not match the anchor image.
By minimizing the distance between images and their correct attribute vectors, while maximizing the distance between images and mismatched attribute vectors, the networks will learn an embedding space where querying with an attribute vector will return the most relevant images.
Note
As shown in the Weak Supervision tutorial, the triplet loss can be replaced by the NT-Xent loss, which is more stable and easier to optimize. Everything that is explained here for the triplet loss can be applied to the NT-Xent loss as well.
Negative selection#
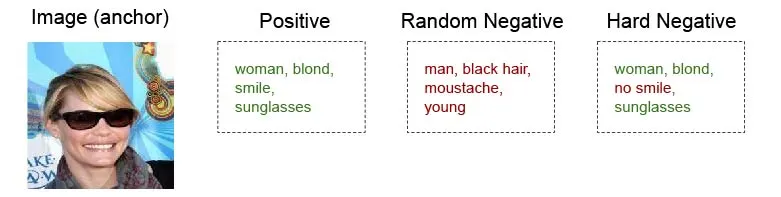
The creation of triplets is a crucial step in training the networks with the triplet loss. To form an anchor-positive pair, you simply take an image and its associated attributes. However, the selection of negatives requires more care. If you randomly sample a negative attribute vector, you risk producing unrealistic attribute combinations (e.g., “woman + blond + with beard”), making it too easy to distinguish positives from negatives. This could lead to poor generalization, as the networks would not learn to differentiate between plausible but incorrect attribute vectors.
A more effective approach to selecting negatives is to sample a random attribute vector from the training data and ensure it differs from the correct attribute vector. This ensures that the negative vector is plausible, making it more challenging for the networks to learn the similarity metric. For even stronger training, you can generate hard negatives by slightly modifying the positive attributes vector, for example, by changing only one to three attributes. Training with hard negatives forces the networks to distinguish between subtle attribute differences, improving their ability to retrieve images that accurately match a given query.
Implementation details#
To implement the triplet loss or the NT-Xent loss, consider referring to the Weak Supervision tutorial for inspiration and guidance. The main difference here is that you have more options for selecting negatives.
You can choose to take all negatives in the batch, similar to the losses used in the weak supervision tutorial. In this case, you must be careful to avoid triplets where the negative attribute vector is identical to the positive attribute vector.
You can choose to craft hard negatives by slightly modifying the positive attribute vector, as described above. In this case, you are not limited to only one negative per anchor-positive pair. You can generate multiple hard negatives by modifying the positive attribute vector in different ways.
You can combine both approaches, taking all negatives in the batch and adding hard negatives. This way, you can benefit from the diversity of negatives in the batch while also training the networks to distinguish between subtle attribute differences.
Recommendation
Start by using all negatives in the batch. Once you have a working system, experiment with hard negatives to see if it improves the retrieval results.
The code below provides a rather efficient way to craft hard negatives. It is a function that takes a batch of attribute vectors and generates hard negatives by changing one to three attributes. You can use this function in your implementation of the loss function with hard negatives.
import torch
def create_hard_negatives(attributes: torch.Tensor, hard_count: int, max_flips: int = 3) -> torch.Tensor:
"""
Create hard negatives by flipping a random subset of attributes.
Args:
attributes : A tensor of shape (N, D) containing 0s and 1s.
hard_count : The number of hard negatives to create per sample.
max_flips : The maximum number of attributes to flip. Defaults to 3.
Returns:
A tensor of shape (N, hard_count, D) containing the hard negatives.
Example:
>>> attributes = torch.tensor([[1, 0, 1, 0, 0], [0, 1, 0, 1, 0]])
>>> create_hard_negatives(attributes, 3)
tensor([[[0., 0., 1., 1., 0.],
[1., 1., 1., 0., 0.],
[1., 0., 1., 0., 1.]],
[[1., 0., 0., 0., 0.],
[1., 1., 1., 1., 1.],
[1., 1., 0., 1., 0.]]])
"""
# Prepare the hard negatives
hard_negatives = attributes.unsqueeze(1).repeat(1, hard_count, 1).bool()
shape = hard_negatives.shape # (N, hard_count, D)
# Randomly select up to 3 attributes to flip
rand_perm = torch.rand(shape, device=attributes.device).argsort(dim=2)[:, :, :max_flips]
# Randomly determine the number of attributes to flip for each sample
num_flips = torch.randint(1, max_flips + 1, (shape[0], shape[1]), device=attributes.device) # (N, hard_count)
# Loop over the number of flips and apply them
for i in range(1, max_flips + 1):
# Create a mask for where we should flip exactly `i` attributes
flip_mask = num_flips == i # (N, hard_count)
if flip_mask.any():
# Get the indices to flip
selected_indices = rand_perm[:, :, :i] # Get the first `i` attribute indices per sample
# Get index positions where we need to flip
batch_indices, hard_indices = torch.nonzero(flip_mask, as_tuple=True)
# Extract corresponding indices from `selected_indices`
selected_attr_indices = selected_indices[batch_indices, hard_indices]
# Apply the flip
hard_negatives[batch_indices.unsqueeze(1), hard_indices.unsqueeze(1), selected_attr_indices] ^= True
return hard_negatives.float()
