Linear algebra

Linear algebra#

NumPy includes many functions for linear algebra in the numpy.linalg package.

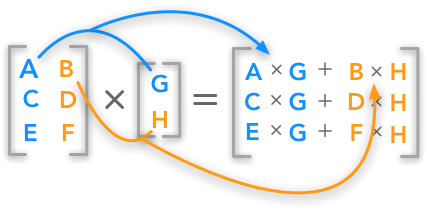
dot-product

import numpy as np

Multiplication#

There are several ways to multiply two vectors. The most natural way is the element-wise product. This works precisely how it sounds: multiply two vectors of the same size element-by-element.

\[\begin{split} \mathbf{x} * \mathbf{y} = \begin{bmatrix} x_1 y_1 \\ \vdots \\ x_{N} y_{N} \\ \end{bmatrix} \end{split}\]

In numpy, this operation is performed by the operator *.

x = np.array([2.1, -5.7, 13])
y = np.array([4.3,  9.2, 13])

p = x * y

print(p)

[  9.03 -52.44 169.  ]

Scalar product#

The scalar product is another way to multiply two vectors of the same dimension. Here is how it works: multiply the vectors element-by-element, then add up the result. For two generic column vectors \(\mathbf{x}\in\mathbb{R}^N\) and \(\mathbf{y}\in\mathbb{R}^N\), the scalar product is mathematically defined as

\[\begin{split} \mathbf{x}^\top \mathbf{y} = \begin{bmatrix}x_1 & \dots & x_{N}\end{bmatrix} \begin{bmatrix}y_1\\\vdots\\y_{N}\end{bmatrix} = x_1 y_1 + \dots + x_{N} y_{N} = \sum_{n=1}^{N} x_n y_n. \end{split}\]

Numpy provides the operator @ and the function np.dot() to do exactly this. It works on arrays of any dimension.

dot = x @ y

print("  x:", x)
print("  y:", y)
print("x@y:", dot)

  x: [ 2.1 -5.7 13. ]
  y: [ 4.3  9.2 13. ]
x@y: 125.59

Matrix-vector product#

The operator @ is also capable of performing matrix-vector or vector-matrix products. Assume that \(A\in\mathbb{R}^{N\times K}\), \({\bf b}\in\mathbb{R}^{K}\), and \({\bf c}\in\mathbb{R}^{N}\):

\[\begin{split} A = \begin{bmatrix} a_{1,1} & \dots & a_{1,K}\\ \vdots & & \vdots\\ a_{N,1} & \dots & a_{N,K}\\ \end{bmatrix} \qquad\qquad {\bf b} = \begin{bmatrix}b_1\\\vdots\\b_{K}\end{bmatrix} \qquad\qquad {\bf c} = \begin{bmatrix}c_1\\\vdots\\c_{N}\end{bmatrix} \end{split}\]

Mathematically, the exact operation performed by @ depends on the order of inputs.

  • A @ b multiplies the vector \({\bf b}\) by the rows of \(A\):

\[\begin{split} A{\bf b} = \begin{bmatrix} \sum_{k=1}^K a_{1,k} b_k \\ \vdots\\ \sum_{k=1}^K a_{N,k} b_k \\ \end{bmatrix}. \end{split}\]

  • c @ A multiplies the vector \({\bf c}\) by the columns of \(A\):

\[ {\bf c}^\top A = \left[ \sum_{n=1}^N a_{n,1} c_n \quad\dots\quad \sum_{n=1}^N a_{n,K} c_n \right]. \]

The result is a vector in both cases.

A = np.array([[1,3,1],[2,5,1]])
b = np.array([1, 1, 1])
c = np.array([1, 1])

Ab = A @ b
cA = c @ A

print("--- A ---")
print(A)
print("--- b ---")
print(b)
print()
print("A @ b:", Ab)
print("c @ A:", cA)

--- A ---
[[1 3 1]
 [2 5 1]]
--- b ---
[1 1 1]

A @ b: [5 8]
c @ A: [3 8 2]

Matrix product#

When both inputs are matrices, the operator @ performs a matrix multiplication. Specifically, given two matrices \(A\in\mathbb{R}^{M\times N}\) and \(B\in\mathbb{R}^{N\times K}\), their product is equal to the scalar product between the rows of \(A\) and the columns of \(B\):

\[\begin{split} AB = \begin{bmatrix} \_\!\_\; {\bf a}_1^\top \,\_\!\_ \\ \vdots\\ \_\!\_\; {\bf a}_M^\top \,\_\!\_ \\ \end{bmatrix} \begin{bmatrix} | & & |\\[-1em] {\bf b}_1 & \dots & {\bf b}_K\\ | & & |\\ \end{bmatrix} = \begin{bmatrix} {\bf a}_1^\top{\bf b}_1 & \dots & {\bf a}_1^\top{\bf b}_K\\ \vdots & & \vdots\\ {\bf a}_M^\top{\bf b}_1 & \dots & {\bf a}_M^\top{\bf b}_K \end{bmatrix}. \end{split}\]
X = np.array([[1,3,1],[2,5,1]])
Y = np.array([[5,1],[9,2],[14,1]])

Z = X @ Y

print("--- X ---")
print(X)
print("--- Y ---")
print(Y)
print("--- X @ Y ---")
print(Z)

--- X ---
[[1 3 1]
 [2 5 1]]
--- Y ---
[[ 5  1]
 [ 9  2]
 [14  1]]
--- X @ Y ---
[[46  8]
 [69 13]]
Contents