Arrays#
A NumPy array stores multiple elements of the same type (usually numbers). It is an object of the class ndarray (alias: array), which provides the following attributes.
.ndimThe number of axes (i.e., dimensions) of the array..shapeA tuple of integers indicating the size of the array in each dimension..sizeThe total number of elements of the array.
There are multiple ways to create and manipulate a NumPy array. Let’s review the basic ones.
import numpy as np
Vectors#
The simplest way to create an array is by passing a list of numbers to np.array(). This produces an array with one axis, which is referred to as vector.
list1 = [0,1,2,3,4]
vector = np.array(list1)
vector
array([0, 1, 2, 3, 4])
Let’s inspect its attributes.
print("ndim:", vector.ndim)
print("shape:", vector.shape)
print("size:", vector.size)
ndim: 1
shape: (5,)
size: 5
From the above, we can deduce that a vector of length \(N\) presents the following attributes:
.ndim = 1.shape = (N,).size = N
In the mathematical language, the notation \(\mathbf{x}\in \mathbb{R}^N\) indicates a vector of size \(N\):
Vectors are conventionally listed out vertically. However, this contrasts with the convention adopted by NumPy, where vectors are listed out horizontally:
Keep that in mind when you implement mathematical expressions in NumPy!
Matrices#
It is also possible to create an array by passing a sequence of lists to np.array(). This produces an array with two axes, which is referred to as matrix.
list2 = [[0,1,2], [3,4,5], [6,7,8]]
matrix = np.array(list2)
matrix
array([[0, 1, 2],
[3, 4, 5],
[6, 7, 8]])
Let’s inspect its attributes.
print("ndim:", matrix.ndim)
print("shape:", matrix.shape)
print("size:", matrix.size)
ndim: 2
shape: (3, 3)
size: 9
A matrix with \(N\) rows and \(M\) columns presents the following attributes:
.ndim = 2.shape = (N, M).size = N*M
In the mathematical language, the notation \(X\in \mathbb{R}^{N\times M}\) indicates a matrix of shape \(N\times M\):
Either axis of a matrix can have length one, thus yielding 2 special cases.
A matrix with one row (and multiple columns):
A matrix with one column (and multiple rows):
To avoid errors and unexpected behaviours, it is crucial to understant the difference between vectors (1d arrays) and rows/columns (2d arrays).
vec = np.array([2,5,9]) # vector (1d array)
row = np.array([[2,5,9]]) # matrix (2d array) with one row
col = np.array([[2],[5],[9]]) # matrix (2d array) with one column
print("----- vector -----")
print(vec, "-> shape:", vec.shape)
print("\n----- matrix (one row) -----")
print(row, "-> shape:", row.shape)
print("\n----- matrix (one col) -----")
print(col, "-> shape:", col.shape)
----- vector -----
[2 5 9] -> shape: (3,)
----- matrix (one row) -----
[[2 5 9]] -> shape: (1, 3)
----- matrix (one col) -----
[[2]
[5]
[9]] -> shape: (3, 1)
Pay attention to this important detail.
The vector has shape
(3,).The single-row matrix has shape
(1,3).The single-column matrix has shape
(3,1).
Visually, you can remark that matrices have a double pair of brackets, whreas vectors only have one pair.
ND arrays#
There is no limit to the nesting level of lists passed to np.array(). The following creates an array with three axes, which is referred to as volume.
list3 = [[[0,1,2], [3,4,5], [6,7,8]], [[4,1,3], [6,1,3], [9,4,5]]]
volume = np.array(list3)
volume
array([[[0, 1, 2],
[3, 4, 5],
[6, 7, 8]],
[[4, 1, 3],
[6, 1, 3],
[9, 4, 5]]])
Let’s inspect its attributes.
print("ndim:", volume.ndim)
print("shape:", volume.shape)
print("size:", volume.size)
ndim: 3
shape: (2, 3, 3)
size: 18
Reshaping#
The shape of an array can be changed with various commands:
.reshape()reconfigures the array into a new shape,.ravel()stretches the array into a vector.
The following are examples of reshaping.
x = np.random.randint(10, size=(3,4))
y = x.reshape(6,2)
z = x.ravel()
print("----- x -----")
print(x, "-> shape:", x.shape)
print("\n----- x.reshape(6,2) -----")
print(y, "-> shape:", y.shape)
print("\n----- x.ravel() -----")
print(z, "-> shape:", z.shape)
----- x -----
[[0 8 7 0]
[2 9 3 6]
[2 9 7 2]] -> shape: (3, 4)
----- x.reshape(6,2) -----
[[0 8]
[7 0]
[2 9]
[3 6]
[2 9]
[7 2]] -> shape: (6, 2)
----- x.ravel() -----
[0 8 7 0 2 9 3 6 2 9 7 2] -> shape: (12,)
The elements of a reshaped array keep the same order in memory as the original array. The order of these elements is “C-style” by default, that is, the rightmost index changes the fastest, so the element after x[0,0] is x[0,1], then x[0,2], and so on.
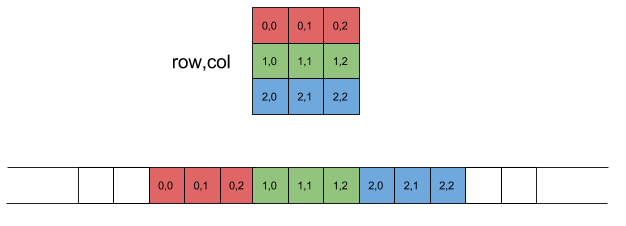
print("original (flattened):", x.flat[:])
print("reshaped (flattened):", y.flat[:])
original (flattened): [0 8 7 0 2 9 3 6 2 9 7 2]
reshaped (flattened): [0 8 7 0 2 9 3 6 2 9 7 2]
Reshaping does not change the number of elements in the original array. If the new shape is not compatible with the original shape, an error is thrown.
z = x.reshape(2,7) # This throws an error
---------------------------------------------------------------------------
ValueError Traceback (most recent call last)
Cell In[13], line 1
----> 1 z = x.reshape(2,7) # This throws an error
ValueError: cannot reshape array of size 12 into shape (2,7)
Reshaping does not make a copy of the data; rather, it produces a new view of the original array (whenever possible). A view behaves like a regular array, except that its elements are shared with the array from which it was created.
a = np.array([4, 10, 7, 2, 5, 1])
b = a.reshape(2,3) # Shared data!
print("----- a -----")
print(a)
print("\n----- b -----")
print(b)
----- a -----
[ 4 10 7 2 5 1]
----- b -----
[[ 4 10 7]
[ 2 5 1]]
Pay attention to this important detail.
The reshaped array shares the same elements of the original array, without making an actual copy of the data (whenever possible). Hence, any modification on the reshaped array is performed on the original array.
b[1,0] = -10 # This also modifies the "original" array
print("----- a -----")
print(a)
print("\n----- b -----")
print(b)
----- a -----
[ 4 10 7 -10 5 1]
----- b -----
[[ 4 10 7]
[-10 5 1]]
To summarize, the functions reshape() and ravel() reconfigure the elements of an array into a new shape, without changing their values. They work according to the following rules.
Shallow copy: The reshaped array shares the same elements with the original array.
Same order: The shared elements keep the same order in memory.
Same size: The total number of elements does not change.
Exercises#
Solve the following exercises on array creation and reshaping. Then, proceed to the next section.
Quiz 1#
Create a vector of length
5, filled with zeros.
Hint: np.zeros()
vector_zeros = None # YOUR CODE HERE
Quiz 2#
Create a matrix with
8rows and4columns, filled with one.
Hint: np.ones()
matrix_ones = None # YOUR CODE HERE
Quiz 3#
Get the number of rows and columns of a matrix.
Hint: .shape
# This is the array to work with
matrix = np.array([[ 1, 2, 3],
[ 4, 5, 6],
[ 7, 8, 9],
[10, 11, 12]])
nrows = None # YOUR CODE HERE
ncols = None # YOUR CODE HERE
Quiz 4#
Propose three different ways to reshape an array into a vector (1d array).
Hints:
# This is the array to work with
volume = np.array([[[5,6,3],
[3,2,7],
[3,5,1]],
[[5,6,3],
[3,2,7],
[3,5,1]]])
flat_vector = None # YOUR CODE HERE
