Indexing#
NumPy arrays can be indexed and sliced over, much like lists and other Python sequences. Specifically, there are three types of indexing available in NumPy: single indexing, slicing, and advanced indexing. The first two are quite similar to what we have seen in Python lists, but the third is a bit more advanced.
import numpy as np
Single indexing#
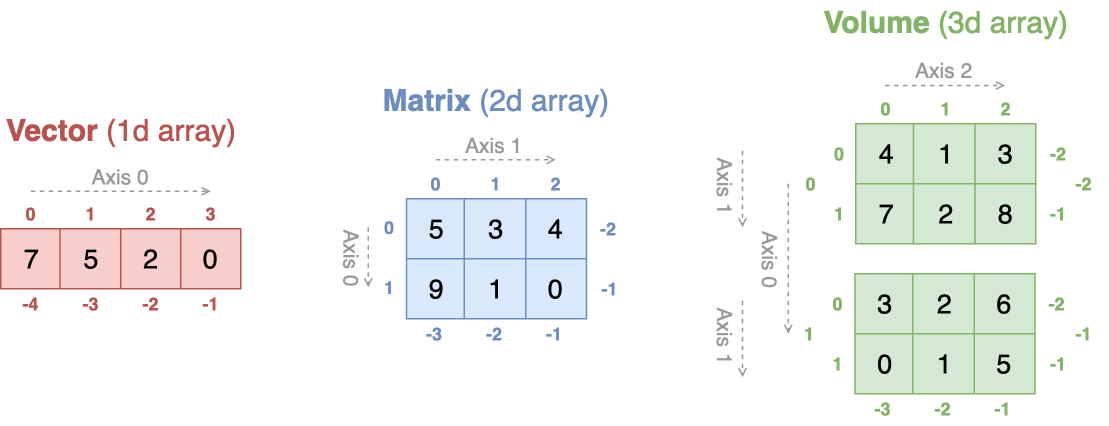
Single-element indexing for a vector (1d array) works exactly like that for other standard Python sequences.
A single element is extracted by giving its position in brackets.
The index must be between
0andsize-1.Negative integers between
-sizeand-1can be used for indexing from the end of the array.
vector = np.array([2.1, -5.7, 2, 9.4, 8])
vector[0]
vector[2]
vector[-1]
print(vector)
print()
print("vector[ 0]:", vector[0])
print("vector[ 2]:", vector[2])
print("vector[-1]:", vector[-1])
[ 2.1 -5.7 2. 9.4 8. ]
vector[ 0]: 2.1
vector[ 2]: 2.0
vector[-1]: 8.0
NumPy also supports indexing for multidimensional arrays.
A single element is accessed by giving a tuple of integers, one for each axis.
For each axis, the integer must be between
(0, shape[n]-1)or(-shape[n], 1).
matrix = np.array([[1,3,4],[2,5,8],[3,1,4],[7,1,9]])
matrix[1, 2]
print(matrix)
print()
print("matrix[1,2]:", matrix[1,2])
[[1 3 4]
[2 5 8]
[3 1 4]
[7 1 9]]
matrix[1,2]: 8
volume = np.array([[[1,3,1],[2,5,1]], [[5,9,0],[5,7,3]]])
volume[1,0,-2]
print(volume)
print()
print("volume[1,0,-2]:", volume[1,0,-2])
[[[1 3 1]
[2 5 1]]
[[5 9 0]
[5 7 3]]]
volume[1,0,-2]: 9
Slicing#
It is possible to extract a contiguous subarray using the slice notation:
vector[start:stop]- items fromstarttostop-1vector[start: ]- items fromstartto the endvector[ :stop]- items from the beginning tostop-1vector[ : ]- all items (from the beginning to the end)
vector[1:3]
vector[ :4]
vector[2: ]
print(vector)
print()
print('vector[1:3] ->', vector[1:3])
print()
print('vector[ :4] ->', vector[:4])
print()
print('vector[2: ] ->', vector[2:])
[ 2.1 -5.7 2. 9.4 8. ]
vector[1:3] -> [-5.7 2. ]
vector[ :4] -> [ 2.1 -5.7 2. 9.4]
vector[2: ] -> [2. 9.4 8. ]
Slicing can be applied to any axis of a multidimensional array, and mixed with other types of indexing.
matrix[2,:]
matrix[1:3,:2]
print(matrix)
print()
print("matrix[2,:] or matrix[2]\n", matrix[2,:])
print()
print("matrix[1:3,:2]\n", matrix[1:3, :2])
[[1 3 4]
[2 5 8]
[3 1 4]
[7 1 9]]
matrix[2,:] or matrix[2]
[3 1 4]
matrix[1:3,:2]
[[2 5]
[3 1]]
Copying vs Sharing#
Slicing does not make a copy of the selected elements; rather, it produces a new view of the original array (whenever possible). A view behaves like a regular array, except that its elements are shared with the array from which it was created.
a = np.array([4, 10, 7, 2, 5])
b = a[1:3] # Shared data!
print("a:", a)
print("b:", b)
a: [ 4 10 7 2 5]
b: [10 7]
Pay attention to this important detail.
Any modification to a “sliced array” is actually performed on the array from which it was created.
b[0] = -1 # this also modifies the "original" array
a: [ 4 -1 7 2 5]
b: [-1 7]
In order to really make a copy of the sliced elements, the method copy() must be explictly called.
a = np.array([4, 10, 7, 2, 5])
b = a[1:3].copy() # Copied data!
b[0] = -1 # this does NOT modify the "original" array
print("a:", a)
print("b:", b)
a: [ 4 10 7 2 5]
b: [-1 7]
Remark. A simple assignment makes neither a copy, nor a view of the original array. It just creates a new alias (i.e., a reference) to the assigned array.
a = np.array([4, 10, 7, 2, 5])
b = a # Same array!
print("Same array:", a is b)
Same array: True
Assigning values to sliced arrays#
Due to how slicing works, it is possible to assign values to a slice of an array. The only constraint is that the values being assigned to the sliced array must be shape consistent (the same shape, or broadcastable to the shape produced by slicing).
x = np.arange(10)
print("x:", x)
x: [0 1 2 3 4 5 6 7 8 9]
For example, it is permitted to assign a constant to a slice.
x[2:7] = -10
print("x:", x)
x: [ 0 1 -10 -10 -10 -10 -10 7 8 9]
Alternatively, it is permitted to assign an array of the right size.
x[2:7] = np.array([10, 20, 30, 40, 50])
print("x:", x)
x: [ 0 1 10 20 30 40 50 7 8 9]
In both cases, the original array x is modified in the positions specified by the slice.
Advanced indexing#
Vectors can be indexed by one array of integers.
The integer array holds the positions of the elements to be extracted.
This array can have an arbitrary size.
The selected values are deep copied into an array with the same shape as the indexing array.
+---+---+---+---+---+
idx = | 1 | 1 | 3 | 8 | 5 |
+---+---+---+---+---+
+------+------+------+------+------+
x[idx] = | x[1] | x[1] | x[3] | x[8] | x[5] |
+------+------+------+------+------+
Here is a concrete example of integer indexing.
np.random.seed(1)
# original vector
x = np.random.randint(0, 10, size=12)
# integer vector of indices
idx = np.array([1,1,3,8,5])
# new vector with the selected values
y = x[idx]
print(" x:", x)
print(" idx:", idx)
print("x[idx]:", y)
x: [5 8 9 5 0 0 1 7 6 9 2 4]
idx: [1 1 3 8 5]
x[idx]: [8 8 5 6 0]
Matrices can be indexed by two arrays of integers.
The indexing arrays hold the row/column positions of the elements to be extracted.
The indexing arrays can be any (broadcastable) shape.
The selected values are deep copied into an array with the same shape as the indexing arrays.
+---+---+---+---+---+
i = | 1 | 1 | 3 | 8 | 5 |
+---+---+---+---+---+
+---+---+---+---+---+
j = | 2 | 4 | 5 | 3 | 7 |
+---+---+---+---+---+
+--------+--------+--------+--------+--------+
X[i,j] = | X[1,2] | x[1,4] | x[3,5] | x[8,3] | x[5,7] |
+--------+--------+--------+--------+--------+
In general, multiple-axis arrays can be indexed by an array of integers for each axis.
a = np.arange(12).reshape(3,4)
i = np.array( [[0,1], [1,2]] ) # indices (2d array) for axis 0
j = np.array( [[2,1], [3,3]] ) # indices (2d array) for axis 1
b = a[i,j] # i and j must have compatible shape
print("----- a -----")
print(a)
print("\n----- i -----")
print(i)
print("\n----- j -----")
print(j)
print("\n----- a[i,j] -----")
print(b)
----- a -----
[[ 0 1 2 3]
[ 4 5 6 7]
[ 8 9 10 11]]
----- i -----
[[0 1]
[1 2]]
----- j -----
[[2 1]
[3 3]]
----- a[i,j] -----
[[ 2 5]
[ 7 11]]
Arrays can be also indexed by one boolean array.
The boolean array indicates both the items to select (
True) and to discard (False).The boolean array must be the same shape as the original array.
The selected elements are deep copied into a return vector (1d array) of smaller size.
+----+----+----+----+----+----+----+----+
x = | x0 | x1 | x2 | x3 | x4 | x5 | x6 | x7 |
+----+----+----+----+----+----+----+----+
0 1 2 3 4 5 6 7
+-------+-------+-------+-------+-------+-------+-------+-------+
mask = | False | True | False | True | False | False | True | True |
+-------+-------+-------+-------+-------+-------+-------+-------+
+----+----+----+----+
x[mask] = | x1 | x3 | x6 | x7 |
+----+----+----+----+
The following are concrete examples of boolean indexing.
np.random.seed(1)
# original vector
x = np.random.randint(0, 10, size=8)
# boolean vector of indices
mask = np.array([False, True, False, True, False, False, True, True])
# new vector with the selected values
y = x[mask]
print(" x:", x)
print(" mask:", mask)
print("x[mask]:", y)
x: [5 8 9 5 0 0 1 7]
mask: [False True False True False False True True]
x[mask]: [8 5 1 7]
matrix = np.arange(12).reshape(3,4)
mask = matrix > 5 # matrix of booleans (same shape)
vector = matrix[mask] # the result is always a vector
print("----- matrix -----")
print(matrix)
print("\n----- mask -----")
print(mask)
print("\n----- vector -----")
print(vector)
----- matrix -----
[[ 0 1 2 3]
[ 4 5 6 7]
[ 8 9 10 11]]
----- mask -----
[[False False False False]
[False False True True]
[ True True True True]]
----- vector -----
[ 6 7 8 9 10 11]
Exercises#
Solve the following exercises on array indexing and slicing. Then, proceed to the next section.
Quiz 8#
Create a vector of size 10 filled with zero, and set the first and last elements to
1.
Remark: The solution can take more than one line of code.
# YOUR CODE HERE
head_tail = None
Quiz 9#
Swap (in-place) the 2nd and 4th element of a vector.
Remark: Single indexing extracts one element from an array. In Python, single values are always copied when assigned to a variable.
# This is the vector to work with
vector = np.array([5, -1, 3, 12, 8, 0])
print("--- before swap ---")
print(vector)
# YOUR CODE HERE
None
print("\n--- after swap ---")
print(vector)
Quiz 10#
Given a matrix, extract the elements indicated in the figure below.
Hint: Recall that you can extract a contiguous part of a matrix via the slicing notation:
matrix[start_row : stop_row : step_row , start_col : stop_col : step_col]

# This is the matrix to work with
matrix = np.array([[ 1, 2, 3],
[ 4, 5, 6],
[ 7, 8, 9],
[10, 11, 12]])
A = None # YOUR CODE HERE
B = None # YOUR CODE HERE
C = None # YOUR CODE HERE
D = None # YOUR CODE HERE
E = None # YOUR CODE HERE
F = None # YOUR CODE HERE
G = None # YOUR CODE HERE
H = None # YOUR CODE HERE
