Operations

Operations#

NumPy provides a large panel of vectorized operations. Vectorization describes the absence of any explicit looping in the code. Operations are applied on every element of the involved arrays in optimized pre-compiled C code. This is the key difference with respect to python lists, which makes NumPy more suitable to scientific computing.

import numpy as np

Binary operations#

Operations that involve two (or more) arrays are applied element-by-element. A new array is created and filled with the result.

\[\begin{split} X+Y=\begin{bmatrix} x_{1,1}+y_{1,1} & x_{1,2}+y_{1,2} & \cdots & x_{1,M}+y_{1,M}\\ x_{2,1}+y_{2,1} & x_{2,2}+y_{2,2} & \cdots & x_{2,M}+y_{2,M}\\ \vdots & \vdots & \ddots & \vdots\\ x_{N,1}+y_{N,1} & x_{N,2}+y_{N,2} & \cdots & x_{N,M}+y_{N,M} \end{bmatrix}. \end{split}\]
a = np.array( [20, 30, 40, 50] )
b = np.array( [ 0,  1,  2,  3] )

c = a + b

print(c)

[20 31 42 53]

The two arrays should be exactly the same size. Errors are thrown if they are not.

a = np.array([1, 2, 3])
b = np.array([2, 2])

c = a * b  # This will give an error when you run it!

---------------------------------------------------------------------------
ValueError                                Traceback (most recent call last)
Cell In[4], line 4
      1 a = np.array([1, 2, 3])
      2 b = np.array([2, 2])
----> 4 c = a * b  # This will give an error when you run it!

ValueError: operands could not be broadcast together with shapes (3,) (2,)

One exception to the above rule is given by operations between an array and a scalar.

a = np.array([1,2,3])
b = 2

c = a * b

print(c)

[2 4 6]

Logical operations are also supported in NumPy.

x = np.array([3, 5, 2, 1, 4, 2])
y = np.array([1, 4, 7, 2, 5, 2])

w = (x > 3) & (y <= x) # "&" --> logical AND
z = (x==2) | (y==1)    # "|" --> logical OR

print("w:", w)
print("z:", z)

w: [False  True False False False False]
z: [ True False  True False False  True]

Unary operations#

Operations that involve one array are applied on all the elements.

x = np.array([[1,3,1],[2,5,1]])

s = x.sum()

print(s)

13

Parameter: axis#

Most of the unary operations return a scalar, because they operate on the array as it were a list of numbers, regardless of its shape. By specifying the axis parameter, you can apply the “reduction” operation along the specified axis of an array. For example:

  • axis=0 applies the operation column-by-column.

  • axis=1 applies the operation row-by-row.

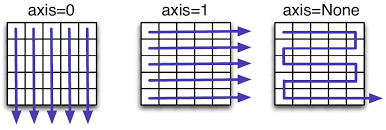
unary

col_sum = x.sum(axis=0)
row_sum = x.sum(axis=1)

print("----- x -----")
print(x, "-> shape:", x.shape)

print("\n----- x.sum(axis=0) -----")
print(col_sum, "-> shape:", col_sum.shape)

print("\n----- x.sum(axis=1) -----")
print(row_sum, "-> shape:", row_sum.shape)

----- x -----
[[1 3 1]
 [2 5 1]] -> shape: (2, 3)

----- x.sum(axis=0) -----
[3 8 2] -> shape: (3,)

----- x.sum(axis=1) -----
[5 8] -> shape: (2,)

Parameter: keepdims#

Note that reduction operations change the dimensions of the array: a matrix becomes a vector.

You can keep all the axes of the original array by setting the keepdims parameter to True.

  • A reduction along axis=0 gives a single-row matrix.

  • A reduction along axis=1 gives a single-column matrix.

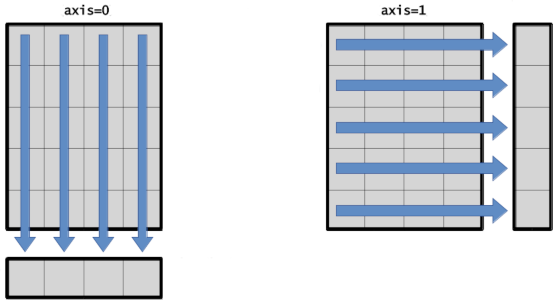
keepdims

col_sum_keep = x.sum(axis=0, keepdims=True)
row_sum_keep = x.sum(axis=1, keepdims=True)

print("----- x -----")
print(x, "-> shape:", x.shape)

print("\n----- x.sum(axis=0, keepdims=True) -----")
print(col_sum_keep, "-> shape:", col_sum_keep.shape)

print("\n----- x.sum(axis=1, keepdims=True) -----")
print(row_sum_keep, "-> shape:", row_sum_keep.shape)

----- x -----
[[1 3 1]
 [2 5 1]] -> shape: (2, 3)

----- x.sum(axis=0, keepdims=True) -----
[[3 8 2]] -> shape: (1, 3)

----- x.sum(axis=1, keepdims=True) -----
[[5]
 [8]] -> shape: (2, 1)

Remark that the shape of the resulting array changes when you specify keepdims=True.

Broadcasting#

The term broadcasting describes how NumPy combines arrays with different shapes during arithmetics operations. As mentioned above, operations on two arrays are performed in an element-by-element fashion. In the simplest case, the arrays must have exactly the same shape.

a = np.array([1, 2, 3])
b = np.array([2, 2, 2])

c = a * b

NumPy’s broadcasting rule relaxes this constraint when the shapes of two arrays meet certain constraints. The simplest example occurs when an array and a scalar value are combined in an arithmetic operation. In this case, the scalar is stretched during the operation, so as to match the shape of the other array.

a = np.array([1,2,3])
b = 2

c = a * b

When operating on two arrays, NumPy compares their shapes element-wise. Subject to certain constraints, the smaller array is “broadcast” across the larger array so that they have compatible shapes. The following are three broadcasting scenarios that often arise in practice.

  • Scalars broadcast to any array.

  • Vectors broadcast to matrices with an equal number of columns.

  • Column matrices broadcast to any vector, and to matrices with an equal number of rows.

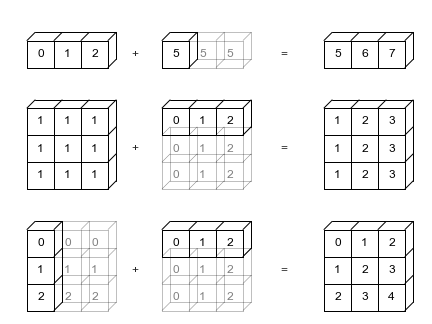
broadcast

A common beginner mistake in NumPy is to unadvertely perform a binary operation with a single-column matrix and a vector. Due to broadcasting, this produces an unexpected result: each element of the former is combined to every element of the latter, resulting in a matrix of shape equal to the two addends:

\[\begin{split} \mathbf{x} + \mathbf{y}^\top = \begin{bmatrix}x_1\\\vdots\\x_{N}\end{bmatrix} + \begin{bmatrix}y_1 & \dots & y_{M}\end{bmatrix} = \begin{bmatrix} x_1+y_1 & \dots & x_1+y_{M}\\ \vdots & & \vdots \\ x_{N}+y_1 & \dots & x_{N}+y_{M} \end{bmatrix}. \end{split}\]
vector = np.array([0,1,2])

column = np.array([[0],[1],[2]])

matrix = column + vector

print("----- vector -----")
print(vector)

print("\n----- column -----")
print(column)

print("\n----- column + vector -----")
print(matrix)

----- vector -----
[0 1 2]

----- column -----
[[0]
 [1]
 [2]]

----- column + vector -----
[[0 1 2]
 [1 2 3]
 [2 3 4]]

Exercises#

Solve the following exercises on array operations. Then, proceed to the next section.

Quiz 5#

Given an array x, compute the following expression:

\[ \log\left(\sum_{i=0}^{N-1} \exp(x_i) \right). \]

Hint:

  • \(\exp(\cdot)\) denotes the exponential, which can be computed in numpy with the function np.exp().

  • \(\sum_i \cdot\) denotes a summation, which can be computed in numpy with the function np.sum().

  • \(\log(\cdot)\) denotes the logarithm, which can be computed in numpy with the function np.log().

# This is the array to work with
x = np.array([7.1, -5.7, 13])

log_sum_exp = None # YOUR CODE HERE

Quiz 6#

Find the minimum and maximum values of a vector.

Hint:

# This is the vector to work with
vector = np.array([5, -1, 3, 12, 8, 0])

min_value = None # YOUR CODE HERE
max_value = None # YOUR CODE HERE

Quiz 7#

Compute the mean value of a matrix, of its rows, and of its columns.

Hint: .mean()

np.random.seed(1)

# This is the matrix to work with
matrix = np.random.randint(10,size=(3,4))

mean_all  = None # YOUR CODE HERE
mean_rows = None # YOUR CODE HERE
mean_cols = None # YOUR CODE HERE
Contents