1.3. Indexing#
NumPy arrays can be indexed and sliced over, much like lists and other Python sequences.
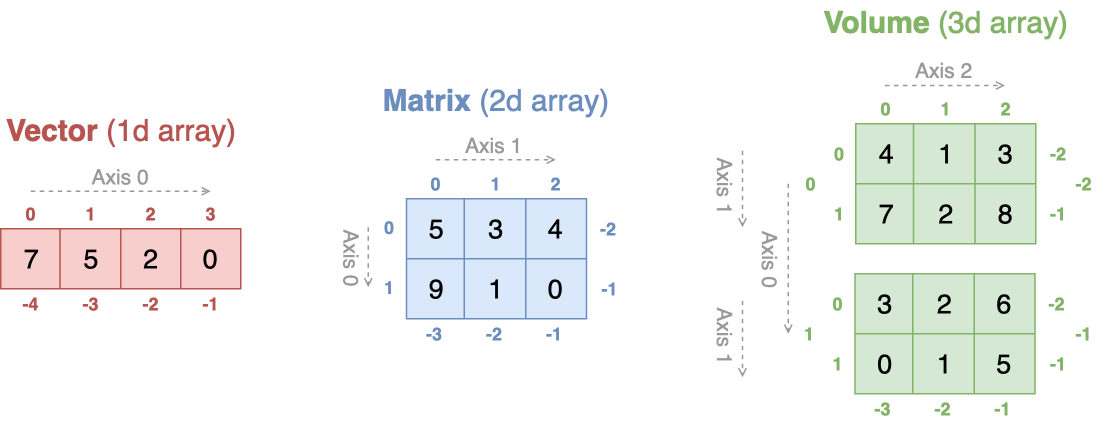
import numpy as np
vector = np.array([2.1, -5.7, 2, 9.4, 8])
matrix = np.array([[1,3,4],[2,5,8],[3,1,4],[7,1,9]])
volume = np.array([[[1,3,1],[2,5,1]], [[5,9,0],[5,7,3]]])
1.3.1. Single indexing#
Indexing for a vector (1d array) is what one would expect.
A single element is extracted by giving its position in brackets.
The index must be between
0andsize-1.Negative integers between
-sizeand-1can be used for indexing from the end of the array.
vector[0]
vector[2]
vector[-1];
+------------+----------------------------+
| vector | [ 2.1 -5.7 2. 9.4 8. ] |
+------------+----------------------------+
| vector[0] | 2.1 |
+------------+----------------------------+
| vector[2] | 2.0 |
+------------+----------------------------+
| vector[-1] | 8.0 |
+------------+----------------------------+
NumPy also supports indexing for multidimensional arrays.
A single element is extracted by giving a tuple of integers, one for each axis.
For each axis, the integer must be between
(0, shape[n]-1)or(-shape[n], 1).
matrix[1, 2]
volume[1, 0, -2];
+-------------+-----------+ +----------------+-------------+
| matrix | [[1 3 4] | | volume | [[[1 3 1] |
| | [2 5 8] | | | [2 5 1]] |
| | [3 1 4] | | | |
| | [7 1 9]] | | | [[5 9 0] |
| | | | | [5 7 3]]] |
+-------------+-----------+ +----------------+-------------+
| matrix[1,2] | 8 | | volume[1,0,-2] | 9 |
+-------------+-----------+ +----------------+-------------+
1.3.2. Slicing#
It is possible to extract a contiguous subarray using the slice notation:
vector[start:stop]- items fromstarttostop-1vector[start: ]- items fromstartto the endvector[ :stop]- items from the beginning tostop-1vector[ : ]- all items (from the beginning to the end)
vector[1:3]
vector[:4]
vector[2:];
+-------------+----------------------------+
| vector | [ 2.1 -5.7 2. 9.4 8. ] |
+-------------+----------------------------+
| vector[1:3] | [-5.7 2. ] |
+-------------+----------------------------+
| vector[ :4] | [ 2.1 -5.7 2. 9.4] |
+-------------+----------------------------+
| vector[2: ] | [2. 9.4 8. ] |
+-------------+----------------------------+
Slicing can be applied to any axis of a multidimensional array, and mixed with other types of indexing.
matrix[2,:]
matrix[1:3, :]
volume[:, 0, :]
volume[:, :, 1:];
+---------------+-----------+ +----------------+-------------+
| matrix | [[1 3 4] | | volume | [[[1 3 1] |
| | [2 5 8] | | | [2 5 1]] |
| | [3 1 4] | | | |
| | [7 1 9]] | | | [[5 9 0] |
| | | | | [5 7 3]]] |
+---------------+-----------+ +----------------+-------------+
| matrix[2,:] | [3 1 4] | | volume[:,0,:] | [[1 3 1] |
| | | | | [5 9 0]] |
+---------------+-----------+ +----------------+-------------+
| matrix[1:3,:] | [[2 5 8] | | volume[:,:,1:] | [[[3 1] |
| | [3 1 4]] | | | [5 1]] |
| | | | | |
| | | | | [[9 0] |
| | | | | [7 3]]] |
+---------------+-----------+ +----------------+-------------+
With fewer indices than dimensions, the missing indices are considered complete slices.
matrix[1]; # equal to 'matrix[1,:]'
+-----------+-----------+
| matrix | [[1 3 4] |
| | [2 5 8] |
| | [3 1 4] |
| | [7 1 9]] |
+-----------+-----------+
| matrix[1] | [2 5 8] |
+-----------+-----------+
1.3.3. Copying vs Sharing#
Slicing does not make a copy of the selected elements; rather, it produces a new view of the original array (whenever possible). A view behaves like a regular array, except that its elements are shared with the array from which it was created.
a = np.array([4, 10, 7, 2, 5])
b = a[1:3] # Shared data!
+--------+------------------+
| a | [ 4 10 7 2 5] |
+--------+------------------+
| b | [10 7] |
+--------+------------------+
| shared | True |
+--------+------------------+
Pay attention to this important detail. Any modification to a “sliced array” is actually performed on the array from which it was created.
b[0] = -1 # this also modifies the "source" array
+---+------------------+
| a | [ 4 -1 7 2 5] |
+---+------------------+
| b | [-1 7] |
+---+------------------+
In order to really make a copy of the sliced elements, the method copy() must be explictly called.
a = np.array([4, 10, 7, 2, 5])
b = a[1:3].copy() # Copied data!
b[0] = -1 # this does not modify the "source" array
+---+------------------+
| a | [ 4 10 7 2 5] |
+---+------------------+
| b | [-1 7] |
+---+------------------+
Remark. A simple assignment makes neither a copy, nor a view of the original array. Technically, it just creates a new alias (i.e., a reference) to the assigned array.
a = np.array([4, 10, 7, 2, 5])
b = a # Same array!
+------+------------------+
| a | [ 4 10 7 2 5] |
+------+------------------+
| b | [ 4 10 7 2 5] |
+------+------------------+
| same | True |
+------+------------------+
1.3.4. Assigning values to sliced arrays#
Due to how slicing works, it is possible to assign values to a slice of an array. The only constraint is that the values being assigned to the sliced array must be shape consistent (the same shape, or broadcastable to the shape produced by slicing).
x = np.arange(10)
+--------+-----------------------+
| x | [0 1 2 3 4 5 6 7 8 9] |
+--------+-----------------------+
| x[2:7] | [2 3 4 5 6] |
+--------+-----------------------+
For example, it is permitted to assign a constant to a slice.
x[2:7] = -10
+--------+-------------------------------------------+
| x | [ 0 1 -10 -10 -10 -10 -10 7 8 9] |
+--------+-------------------------------------------+
| x[2:7] | [-10 -10 -10 -10 -10] |
+--------+-------------------------------------------+
Alternatively, it is permitted to assign an array of the right size.
x[2:7] = np.arange(10,60,10) # [10, 20, 30, 40, 50]
+--------+---------------------------------+
| x | [ 0 1 10 20 30 40 50 7 8 9] |
+--------+---------------------------------+
| x[2:7] | [10 20 30 40 50] |
+--------+---------------------------------+
1.3.5. Advanced indexing#
Vectors can be indexed by one array of integers.
The integer array holds the positions of the elements to be extracted.
This array can have an arbitrary size.
The selected values are deep copied into an array with the same shape as the indexing array.
+---+---+---+---+---+
idx = | 1 | 1 | 3 | 8 | 5 |
+---+---+---+---+---+
+------+------+------+------+------+
x[idx] = | x[1] | x[1] | x[3] | x[8] | x[5] |
+------+------+------+------+------+
Here is a concrete example of integer indexing.
np.random.seed(1)
# original vector
x = np.random.randint(0, 10, size=12)
# integer vector of indices
idx = np.array([1,1,3,8,5])
# new vector with the selected values
y = x[idx]
+--------+---------------------------+
| x | [5 8 9 5 0 0 1 7 6 9 2 4] |
+--------+---------------------------+
| idx | [1 1 3 8 5] |
+--------+---------------------------+
| x[idx] | [8 8 5 6 0] |
+--------+---------------------------+
Matrices can be indexed by two arrays of integers.
The indexing arrays hold the row/column positions of the elements to be extracted.
The indexing arrays can be any (broadcastable) shape.
The selected values are deep copied into an array with the same shape as the indexing arrays.
+---+---+---+---+---+
i = | 1 | 1 | 3 | 8 | 5 |
+---+---+---+---+---+
+---+---+---+---+---+
j = | 2 | 4 | 5 | 3 | 7 |
+---+---+---+---+---+
+--------+--------+--------+--------+--------+
X[i,j] = | X[1,2] | x[1,4] | x[3,5] | x[8,3] | x[5,7] |
+--------+--------+--------+--------+--------+
In general, multiple-axis arrays can be indexed by an array of integers for each axis.
a = np.arange(12).reshape(3,4)
i = np.array( [[0,1], [1,2]] ) # indices (2d array) for axis 0
j = np.array( [[2,1], [3,3]] ) # indices (2d array) for axis 1
b = a[i,j] # i and j must have compatible shape
+--------+-----------------+
| a | [[ 0 1 2 3] |
| | [ 4 5 6 7] |
| | [ 8 9 10 11]] |
+--------+-----------------+
| i | [[0 1] |
| | [1 2]] |
+--------+-----------------+
| j | [[2 1] |
| | [3 3]] |
+--------+-----------------+
| a[i,j] | [[ 2 5] |
| | [ 7 11]] |
+--------+-----------------+
Arrays can be also indexed by one boolean array.
The boolean array indicates both the items to select (
True) and to discard (False).The boolean array must be the same shape as the original array.
The selected elements are deep copied into a return vector (1d array) of smaller size.
+----+----+----+----+----+----+----+----+
x = | x0 | x1 | x2 | x3 | x4 | x5 | x6 | x7 |
+----+----+----+----+----+----+----+----+
0 1 2 3 4 5 6 7
+-------+-------+-------+-------+-------+-------+-------+-------+
mask = | False | True | False | True | False | False | True | True |
+-------+-------+-------+-------+-------+-------+-------+-------+
+----+----+----+----+
x[mask] = | x1 | x3 | x6 | x7 |
+----+----+----+----+
The following are concrete examples of boolean indexing.
np.random.seed(1)
# original vector
x = np.random.randint(0, 10, size=8)
# boolean vector of indices
mask = np.array([False, True, False, True, False, False, True, True])
# new vector with the selected values
y = x[mask]
+---------+---------------------------------------------------+
| x | [5 8 9 5 0 0 1 7] |
+---------+---------------------------------------------------+
| mask | [False True False True False False True True] |
+---------+---------------------------------------------------+
| x[mask] | [8 5 1 7] |
+---------+---------------------------------------------------+
matrix = np.arange(12).reshape(3,4)
mask = matrix > 5 # matrix of booleans (same shape)
vector = matrix[mask] # the result is always a vector
+--------+-----------------------------+
| matrix | [[ 0 1 2 3] |
| | [ 4 5 6 7] |
| | [ 8 9 10 11]] |
+--------+-----------------------------+
| mask | [[False False False False] |
| | [False False True True] |
| | [ True True True True]] |
+--------+-----------------------------+
| vector | [ 6 7 8 9 10 11] |
+--------+-----------------------------+
