5.4.9. Positive L2-ball

For a given scalar \(\xi \ge 0\), the positive L2-ball is a convex constraint defined as

\[ \mathcal{C}_{L_2^+} = \big\{ {\bf w} \in \mathbb{R}^{N} \;|\; {\bf w} \ge 0,\; \|{\bf w}\|_2 \le \xi \big\}, \]

where \(\|{\bf w}\|_2 = \sqrt{w_1^2+\dots+w_N^2}\) is the L2-norm. The condition \(\xi \ge 0\) is required for this subset to be nonempty. The figure below shows how this constraint looks like in \(\mathbb{R}^{2}\) or in \(\mathbb{R}^{3}\).

Positive L2-ball in 2D

Positive L2-ball in 3D

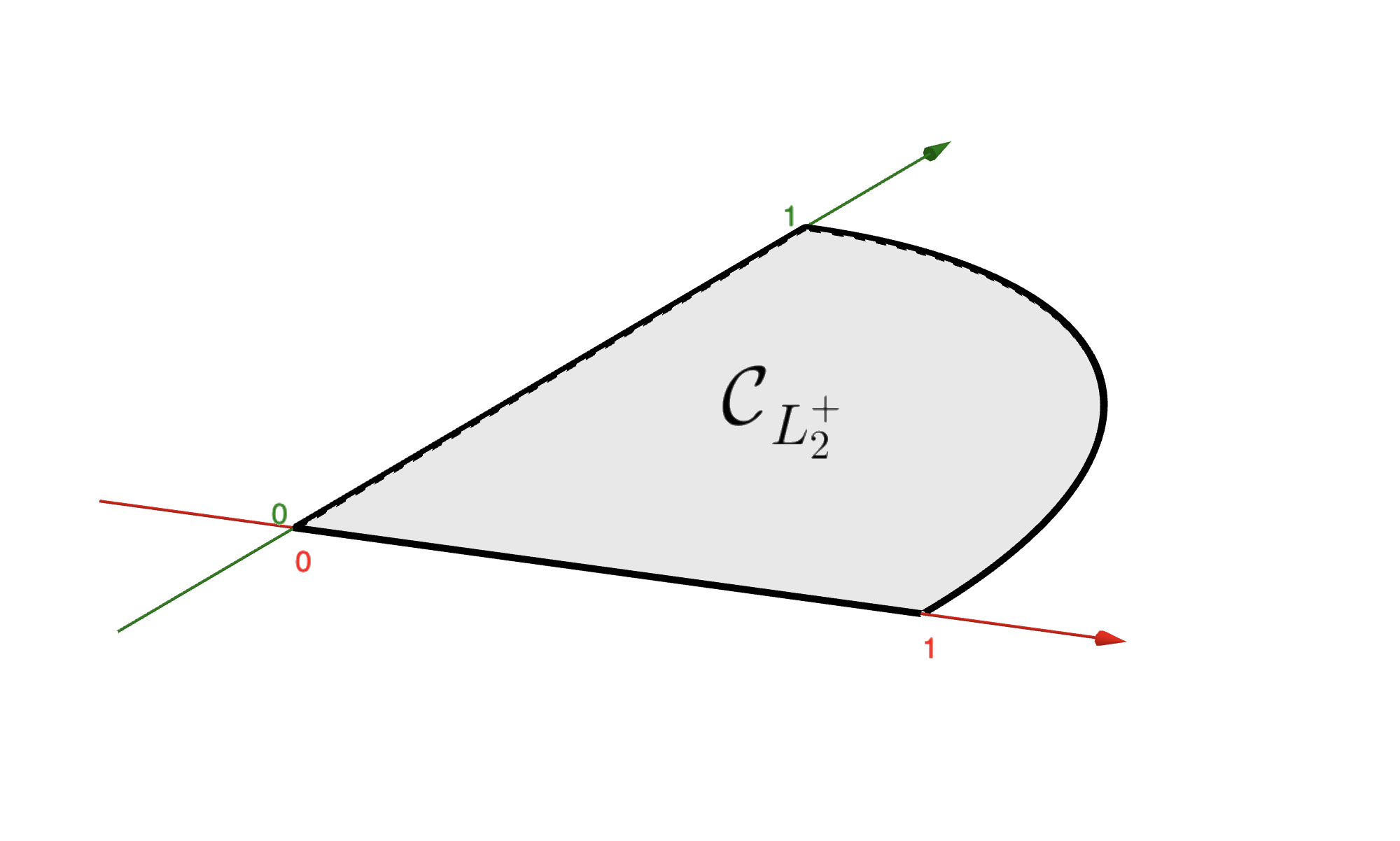
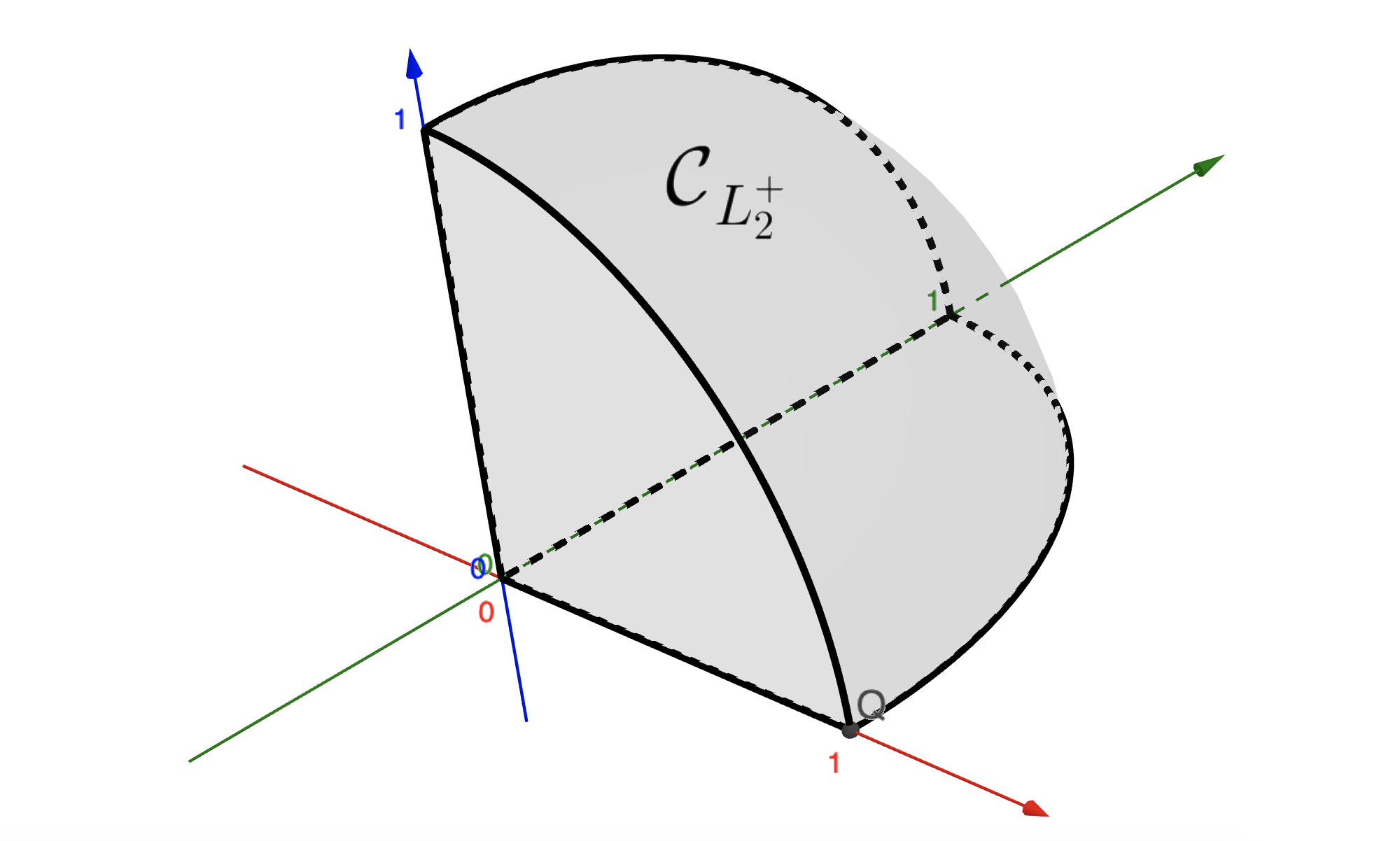
5.4.9.1. Constrained optimization

Optimizing a function \(J({\bf w})\) subject to the positive L2-ball constraint can be expressed as

\[\begin{split} \operatorname*{minimize}_{\textbf{w}\in\mathbb{R}^N}\; J({\bf w}) \quad{\rm s.t.}\quad \begin{cases} {\bf w} \ge 0 \\ \|{\bf w}\|_2 \le \xi. \end{cases} \end{split}\]

The figure below visualizes such an optimization problem in \(\mathbb{R}^{2}\).

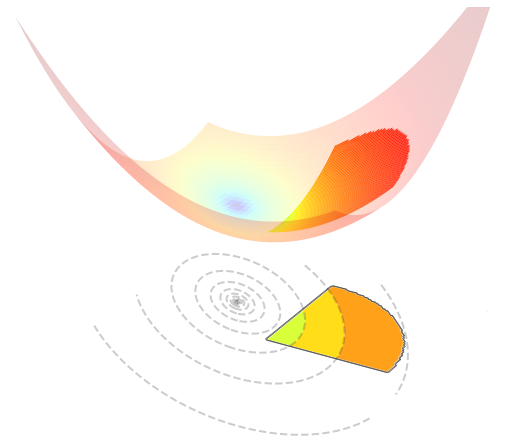
5.4.9.2. Orthogonal projection

The projection of a point \({\bf u}\in\mathbb{R}^{N}\) onto the positive L2-ball is the (unique) solution to the following problem

\[\begin{split} \operatorname*{minimize}_{{\bf w}\in\mathbb{R}^N}\; \|{\bf w}-{\bf u}\|^2 \quad{\rm s.t.}\quad \begin{cases} {\bf w} \ge 0 \\ \|{\bf w}\|_2 \le \xi. \end{cases} \end{split}\]

The solution can be computed as follows.

Projection onto the positive L2-ball

\[ \mathcal{P}_{\mathcal{C}_{L_2^+}}({\bf u}) = \mathcal{P}_{\mathcal{C}_{L_2}}\big(\max\{{\bf u},{\bf 0}\}\big) \]

Note: \(\mathcal{C}_{L_2}\) denotes the standard L2-ball.

5.4.9.3. Implementation

The python implementation is given below.

def project_l2plus(u, bound):
    return project_l2ball(np.maximum(0, u), bound)

Here is an example of use.

u = np.array([-1, 2, -5, 3, 2])

p = project_l2plus(u, bound=5)