Convergence analysis

Gradient descent is guaranteed to find a stationary point of a function under very mild assumptions. To mathematically prove the convergence, it is required that the function is bounded below and Lipschitz differentiable. In a nutshell, the proof is based on the following reasoning.

• Recall that gradient descent generates the points \({\bf w}_{k+1} = {\bf w}_k - \alpha \nabla J({\bf w}_k)\) for some initialization \({\bf w}_0\).

• If the gradient is \(L\)-Lipschitz continous, the choice of step-size \(\alpha < \frac{2}{L}\) guarantees a decrease \(J({\bf w}_{k+1}) < J({\bf w}_{k})\) at each iteration \(k=0,1,\dots\), unless \({\bf w}_{k}\) is a stationary point in which case the algorithm stops by itself.

• If the function is lower bounded, \(J({\bf w}_{k})\) cannot be decreased below the minimum value.

• So, \(\|\nabla J({\bf w}_k)\|^2\) must necessarily go to zero as \(k\to+\infty\).

Now, let’s develop the maths behind this result.

Lipschitz differentiability

A differentiable function \(J({\bf w})\) is said to be Lipschitz differentiable if there exists some \(L>0\) such that

\[ (\forall {\bf x}\in\mathbb{R}^N)(\forall {\bf y}\in\mathbb{R}^N) \qquad \|\nabla J({\bf x}) - \nabla J({\bf y}) \| \le L \|{\bf x} - {\bf y} \|. \]

Note that the above definition does not assume convexity. For a twice-differentiable function \(J({\bf w})\), the gradient \(\nabla J({\bf w})\) is Lipschitz continuous if and only if the eigenvalues of the Hessian matrix \(\nabla^2 J({\bf w})\) are upper bounded by a finite constant

\[ L = \sup_{\mathbf{w}} \|\nabla^2 J({\bf w})\|_2 < +\infty. \]

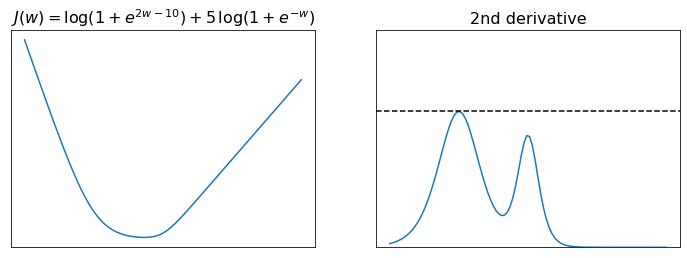
The figure below plots the function \(J(w) = \log\left(1+e^{2w-10}\right) + 5\log\left(1+e^{-w}\right)\) and its second derivative. You can see that \(J''(w)\) is upper bounded by the constant \(L=5/4\). Hence, the first derivative is Lipschitz continuous, which intuitively means that \(J'(w)\) is limited in how fast it can change, or equivalently that the function \(J(w)\) has bounded curvature.

Descent lemma

Let us consider a twice-differentiable function \(J(w)\) of scalar variable \(w\in\mathbb{R}\). According to Taylor’s Remainder Theorem, there exists a point \(\xi\) in the interval delimited by \(w\) and \(p\) such that

\[ J(w) = J(p) + J'(p)(w-p) + \frac{J''(\xi)}{2} (w-p). \]

If the derivative of \(J(w)\) is \(L\)-Lipschitz continuous, then \(J''(\xi) \le L\) by definition. It follows that \(J(w)\) is majorized by a quadratic function with curvature \(1/L\), namely

\[ (\forall w\in\mathbb{R})(\forall p\in\mathbb{R}) \qquad J(w) \le J(p) + J'(p)(w-p) + \frac{L}{2} (w-p). \]

This result can be generalized to a differentiable function \(J({\bf w})\) of vector variable \({\bf w}\in\mathbb{R}^N\). Recall that a quadratic approximation of \(J\) around the point \({\bf p}\in\mathbb{R}^N\) with symmetric curvature \(\alpha>0\) reads

\[ Q_{\alpha}\left(\mathbf{w}\,|\,\mathbf{p}\right) = J\left(\mathbf{p}\right) + \nabla J\left(\mathbf{p}\right)^\top\left(\mathbf{w}-\mathbf{p}\right)+\frac{1}{2\alpha}\left\Vert \mathbf{w}-\mathbf{p}\right\Vert^{2}. \]

The descent lemma says that

\[\begin{split} \begin{cases} \textrm{$\nabla J$ is Lipschitz}\\ \textrm{continuous with}\\ \textrm{constant $L$} \end{cases} \qquad \Longrightarrow \qquad (\forall \mathbf{w},\forall\mathbf{p}) \quad J\left(\mathbf{w}\right) \le Q_{1/L}\left(\mathbf{w}\,|\,\mathbf{p}\right). \end{split}\]

This idea is illustrated below for the function introduced in the previous example. For each tangency point \(p\) (marked as a red dot), you can see that the quadratic approximation \(Q_{1/L}\left(\cdot\,|\,p\right)\) with Lipschitz curvature (shown in light blue) always lies completely above the function (shown in black), and that \(p\) is the unique point where they touch, i.e., \(Q_{\alpha}\left(p\,|\,p\right) = J(p)\).

Sufficient descent condition

Consider the sequence of points generated by gradient descent

\[ {\bf w}_{k+1} = {\bf w}_k - \alpha \nabla J({\bf w}_k). \]

How small should the step-size be to ensure a strict descent at each iteration? We can use the descent lemma to answer this question. First, we evaluate the point \({\bf w}_{k+1}\) on the Lipschitz quadratic majorizer that is tangent to \({\bf w}_{k}\), yielding

\[\begin{split} \begin{aligned} Q_{1/L}\left(\mathbf{w}_{k+1}\,|\,\mathbf{w}_k\right) &= J\left(\mathbf{w}_k\right) + \nabla J\left(\mathbf{w}_k\right)^\top\left(\mathbf{w}_{k+1}-\mathbf{w}_{k}\right)+\frac{L}{2}\left\Vert \mathbf{w}_{k+1}-\mathbf{w}_k\right\Vert^{2} \\ &= J\left(\mathbf{w}_k\right) + \nabla J\left(\mathbf{w}_k\right)^\top\big(- \alpha \nabla J({\bf w}_k)\big)+\frac{L}{2}\left\Vert - \alpha \nabla J({\bf w}_k) \right\Vert^{2} \\ &= J\left(\mathbf{w}_k\right) -\alpha \| \nabla J\left(\mathbf{w}_k\right) \|^2 + \frac{\alpha^2 L}{2}\left\Vert \nabla J({\bf w}_k) \right\Vert^{2} \\ &= J\left(\mathbf{w}_k\right) - \alpha\left(1-\frac{\alpha L}{2}\right) \| \nabla J\left(\mathbf{w}_k\right) \|^2. \end{aligned} \end{split}\]

Then, we use the descent lemma to establish that \(J({\bf w}_{k+1}) \le Q_{1/L}\left(\mathbf{w}_{k+1}\,|\,\mathbf{w}_k\right) \), from which we derive the inequality

\[ J\left(\mathbf{w}_{k+1}\right) \le J\left(\mathbf{w}_k\right) - \alpha\left(1-\frac{\alpha L}{2}\right) \| \nabla J\left(\mathbf{w}_k\right) \|^2. \]

This condition allows us to conclude that if the step size is small enough, the value of the cost function will decrease at each iteration of gradient descent, unless we are at a stationary point where the gradient is zero:

\[ 0<\alpha<\frac{2}{L} \qquad \Longrightarrow \qquad J\left(\mathbf{w}_{k+1}\right) < J\left(\mathbf{w}_{k}\right) \;\;\textrm{if $\nabla J\left(\mathbf{w}_k\right)\neq{\bf 0}$}. \]

This idea is illustrated below for the function \(J(w)\) introduced in the previous example. For a given point \(w_k\) (marked as a red dot), gradient descent computes the next point \(w_{k+1} = w_k -\alpha J'(w_k)\) (marked as a green dot), where the value of \(\alpha\) is controlled by the slider. The choice \(\alpha=\frac{1}{L}\) leads to \(w_{k+1}\) being the minimum of the quadratic majorizer \(Q_{1/L}(\cdot\,|\,w_k)\), whereas the choice \(\alpha=\frac{2}{L}\) leads to \(w_{k+1}\) being the point such that \(Q_{1/L}(w_{k+1}\,|\,w_k) = Q_{1/L}(w_{k}\,|\,w_k)\). The descent lemma guarantees a decrease \(J\left(\mathbf{w}_{k+1}\right) < J\left(\mathbf{w}_{k}\right)\) for all \(\alpha < \frac{2}{L}\), based on the fact that \(Q_{1/L}(w\,|\,w_k)\) is a majorant of \(J(w)\). In this particular example, however, you can observe that a decrease \(J\left(\mathbf{w}_{k+1}\right) < J\left(\mathbf{w}_{k}\right)\) also occurs for step-sizes much larger than the theoretical limit derived from the descent lemma. This happens because the Lipschitz majorant \(Q_{1/L}(w\,|\,w_k)\) is quite a poor approximation of the function \(J(w)\). Consequently, the choice of step-size \(\alpha<\frac{2}{L}\) is a sufficient but not necessary condition for decreasing the cost function at each iteration of gradient descent.

Convergent series of gradients

The sufficient descent condition ensures that the progress made by each iteration of gradient descent is lower bounded by

\[ \alpha\left(1-\frac{\alpha L}{2}\right) \| \nabla J\left(\mathbf{w}_k\right) \|^2 \le J\left(\mathbf{w}_k\right) - J\left(\mathbf{w}_{k+1}\right). \]

In particular, the guaranteed progress is maximized with the choice \(\alpha=\frac{1}{L}\), leading to

\[ \frac{1}{2L} \| \nabla J\left(\mathbf{w}_k\right) \|^2 \le J\left(\mathbf{w}_k\right) - J\left(\mathbf{w}_{k+1}\right). \]

Note that the progress is all the smaller when greater is the Lipschitz constant \(L\). Nevertheless, we can prove that gradient descent converges to a stationary point by checking that \(\| \nabla J\left(\mathbf{w}_k\right) \|^2 \to 0\) as \(k\to+\infty\). Let’s start by summing up the squared norms of all the gradients up to \(T\) iterations:

\[ \frac{1}{2L} \sum_{k=0}^T \| \nabla J\left(\mathbf{w}_k\right) \|^2 \le \sum_{k=0}^T \Big( J\left(\mathbf{w}_k\right) - J\left(\mathbf{w}_{k+1}\right) \Big). \]

On the right-hand side, we have a telescopic sum that is equal to

\[ \sum_{k=0}^T \Big( J\left(\mathbf{w}_k\right) - J\left(\mathbf{w}_{k+1}\right) \Big) = J\left(\mathbf{w}_0\right) - J\left(\mathbf{w}_{1}\right) + J\left(\mathbf{w}_1\right) \dots -J\left(\mathbf{w}_T\right) + J\left(\mathbf{w}_T\right) - J\left(\mathbf{w}_{T+1}\right) = J\left(\mathbf{w}_0 \right) - J\left(\mathbf{w}_{T+1}\right). \]

Now, we need a second assumption: the function must be bounded below. In this case, there exists a finite value \(J^*\) such that \(J^* \le J\left(\mathbf{w}\right)\) for every point \(\mathbf{w}\). We can thus write \(J^*\le J\left(\mathbf{w}_{T+1}\right)\) or \( -J\left(\mathbf{w}_{T+1}\right) \le -J^*\), which leads to

\[ J\left(\mathbf{w}_0 \right) - J\left(\mathbf{w}_{T+1}\right) \le J\left(\mathbf{w}_0 \right) - J^*. \]

Consequently, the sum of gradients is upper bounded by a finite positive value

\[ \sum_{k=0}^T \| \nabla J\left(\mathbf{w}_k\right) \|^2 \le 2L\Big( J\left(\mathbf{w}_0 \right) - J^* \Big). \]

By taking the limit for \(T\to+\infty\), we deduce that the gradients yield a convergent series

\[ \sum_{k=0}^{+\infty} \| \nabla J\left(\mathbf{w}_k\right) \|^2 < +\infty, \]

from which we necessarily conclude that \(\| \nabla J\left(\mathbf{w}_k\right) \|^2 \to 0\) as \(k\to+\infty\).