5.3. Geometric optimality#
Constrained optimization aims at finding a minimum of the function \(J({\bf w})\) on the feasible set \(\mathcal{C}\subset \mathbb{R}^N\), formally denoted as
The solutions to a constrained optimization problem can be precisely characterized by putting the gradient of \(J({\bf w})\) in relation to the topology of \(\mathcal{C}\), yielding what are called the first-order constrained optimality conditions.
5.3.1. Constrained minimum#
A point \({\bf w}^\star\!\in\mathcal{C}\) that gives the smallest value of \(J({\bf w})\) on the set \(\mathcal{C}\) is called constrained “global” minimum.
Constrained “global” minimum
Constrained “local” minimum
The goal of constrainted optimization is to retrieve a solution that is globally optimal. This may not always be possible, depending on the “difficulty” of a given problem. In such cases, we are forced to settle for a solution that is only locally optimal. In this regard, a constrained “local” minimum is a point \({\bf \bar{w}}\in\mathcal{C}\) that gives the smallest value of \(J({\bf w})\) on the intersection of \(\mathcal{C}\) with a sufficiently small neighbor \(\mathcal{B}_r\) of \({\bf \bar{w}}\), namely
By definition, a constrained minimum occurs
either at a proper minimum of the function \(J({\bf w})\) - if such minimum belongs to \(\mathcal{C}\),
or at the boundary of the feasible set \(\mathcal{C}\) - if none of the function’s proper minima belong to \(\mathcal{C}\).
Both of these situations are illustrated in the figure below. In the left panel, the proper minimum of \(J({\bf w})\) belongs to \(\mathcal{C}\), and thus it is also the constrained minimum of \(J({\bf w})\) on \(\mathcal{C}\). In the right panel, the proper minimum of \(J({\bf w})\) does not belong to \(\mathcal{C}\), hence it cannot be the constrained minimum of \(J({\bf w})\) on \(\mathcal{C}\). The latter is instead located somewhere at the boundary of \(\mathcal{C}\).
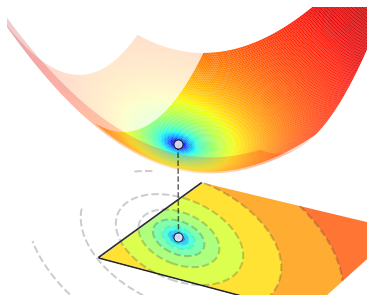
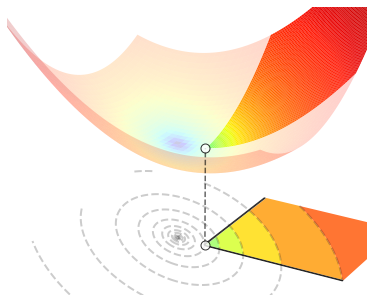
A solution to a constrained optimization problem may not always exist. The foremost assumption in constrained optimization is that the feasible set \(\mathcal{C}\) must be nonempty and closed, so as to ensure that \(\mathcal{C}\) contains its boundary. Hovewer, this is usually not enough to guarantee the existence of a constrained minimum, and some additional hypotheses are required on both the function \(J({\bf w})\) and the feasible set \(\mathcal{C}\), such as the following ones. [1]
Existence of constrained minima
This is a sufficient condition. A constrained minimum may exist even if the above assumptions do not hold.
5.3.2. Geometric insights#
Constrained optimization is based on the following intuition. If the point \({\bf w}^\star\in\mathcal{C}\) is a minimum of \(J({\bf w})\) on \(\mathcal{C}\), then it should not be possible to decrease the function along any path inside \(\mathcal{C}\) starting at \({\bf w}^\star\). Since the function can be locally decreased by moving in any direction whose angle is less than \(90°\) with respect to the negative gradient \(-\nabla J({\bf w})\), optimality occurs only in two different cases:
either the gradient \(\nabla J({\bf w}^\star)\) is zero,
or the negative gradient \(-\nabla J({\bf w}^\star)\) is orthogonal to \(\mathcal{C}\) at \({\bf w}^\star\).
Such concept is illustrated in the following examples.
Note
A function decreases locally in any direction whose angle is less than \(90°\) to the negative gradient.
5.3.2.1. Constraint with “smooth” boundary#
The figure below presents the constrained optimization problem
Since the function’s smallest point falls outside the constraint, the constrained minimum lies on the boundary (white dot). By moving the slider from left to right, you can visualize the negative gradient (black/red arrow) on differents points of the boundary (red dot). The constrained minimum is the point where the negative gradient forms a 90° angle with the line tangent to the constraint at that point (green line). This condition ensures that the function cannot be further decreased by moving to any other point that satisfies the constraint.
Note
The gradient \(\nabla J({\bf w})\) is always orthogonal to the contour lines of \(J({\bf w})\).
