4.3. First-order optimality

The notion of derivative codifies the local behavior of a differentiable function. This information can be thus used to characterize its minima, yielding what is called the first-order optimality condition. While there are a few important instances when this mathematical tool can be used to directly determine the solutions to an optimization problem, the first-order optimality condition motivates the construction of optimization algorithms like the gradient descent method.

4.3.1. Necessary optimality condition

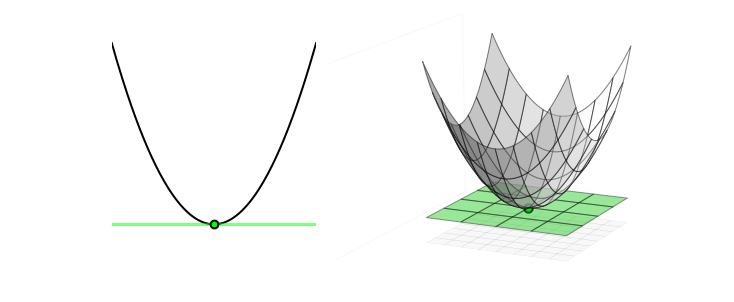
The next figure shows a quadratic function in one and two dimensions. In each panel, the global minimum is marked with a green point, and the tangent at such point is plotted with green line or plane. You can see that the tangents are perfectly flat, indicating that the first derivatives at those points are zero. Such behavior is universal: the gradient is always zero at the minima of a function. This is because the minima of a function are naturally located at “valley floors”, where the tangent to the function is perfectly flat, and thus has zero slopes there. Since the gradient at a point gives precisely this slope information, it provide a convenient way of characterizing the minima of a function, summarized as follows.

First-order optimality (necessary)

\[ \textrm{${\bf w}^\star$ is a global minimum} \quad\Rightarrow\quad \nabla J({\bf w}^\star) = {\bf 0}.\]

4.3.2. Stationary points

The first-order necessary optimality condition provides a very useful characterization of minima. But there is a catch: the optimality is expressed as an implication, rather than an equivalence! This means that not all the points with zero gradient are minima. In general, there exists a variety of points in which the gradient is zero, such as:

• local and global minima,

• local and global maxima,

• saddle points.

All together, they are referred to as stationary points.

Stationary point

\[ \textrm{${\bf\bar{w}}$ is a stationary point} \quad\iff\quad \nabla J({\bf\bar{w}}) = {\bf 0} \]

The following figure draws the first derivative of a function by moving the slider to the right. It is interesting to take notice of all the points where the first derivative passes through the zero: these are the function’s stationary points, among which there is the global minimum at \(w^\star=1\). Note also that the function is continuously differentiable.

Here is another example, where the gradient vanishes at the saddle point \(\bar{w}=0\).

4.3.3. Sufficient optimality condition

Optimization problems are not born equal! It is very important to determine whether the cost function is convex or nonconvex. As explained in a previous chapter, convex functions are “curved up” without any bends the other way. Why do we care about convexity? Because a differentiable function is convex if and only if its graph lies above all of its tangents at every point of the domain. This property is illustrated in the figure below.

The tangency behavior depicted in the previous figure can be mathematically expressed as

\[ \textrm{$J({\bf w})$ is convex} \qquad\iff\qquad \big(\forall{\bf w},{\bf \bar{w}}\big) \quad J({\bf w}) \ge J({\bf \bar{w}}) + \nabla J({\bf \bar{w}})^\top({\bf w}-{\bf \bar{w}}). \]

Note that this inequality turns into the definition of global minimum when \(\nabla J({\bf \bar{w}})=0\). Therefore, all the stationary points of a convex function are global minima.

First-order optimality (sufficient)

\[ \textrm{$J$ is convex and $\nabla J({\bf w^\star}) = {\bf 0}$} \qquad\Rightarrow\qquad \textrm{${\bf w^\star}$ is a global minimum}. \]

The following figure plots the first derivative of a convex function by moving the slider to the right. Remark that the first derivative only vanishes at the global minimum. More generally, the first derivative of a convex function is non-decreasing. This means that a convex function may have an infinite number of minima, but they necessarily form a convex set.