3. Building a tetris AI#
Tetris is a popular video game created by Alexey Pajitnov in 1985. The game is played on a grid originally composed of 20 rows and 10 columns, where pieces of 7 different shapes fall from the top. The player has to choose where to place each falling piece by moving it horizontally and rotating it. When a row is filled, it is removed and all the cells above it move one line down. The goal is to remove as many rows as possible. The game is over when there is no space available at the top of the grid for the new piece.
In the following, we consider the variation of the game in which the player knows only the current falling piece. This game constitutes an interesting optimization benchmark in which the goal is to find a policy that maximizes the number of lines removed in a game. This optimization problem is known to be computationally hard. It contains a huge number of board configurations (about \(2^{200} \approx 1.6 \times 10^{60}\)), and even in the case that the sequence of pieces is known in advance, finding the optimal strategy is an NP-hard problem.
3.1. Placing the falling tetromino#
When the AI plays the game, it is presented with a board and a new tetromino, and tries to make a decision about where to place the tetromino. The latter can be placed on the game board in many ways, with different rotations and translations. Some of these placements are favorable, and others are disadvantageous. In order to decide which placements are good and which are bad, the AI must try every possible placement and choose the one with the best score, according to the scoring system discussed in the next section. As the goal is to clear as many lines as possible, the scoring system must be able to find a suitable placement for the current tetromino, and make sure that subsequent tetrominoes can be placed favorably.
The figure below illustrates the process of iterating through every possible placement of a tetromino. Note that the total number of possible placements depends both on the falling tetromino and the current board. The maximum number of placements is 32.
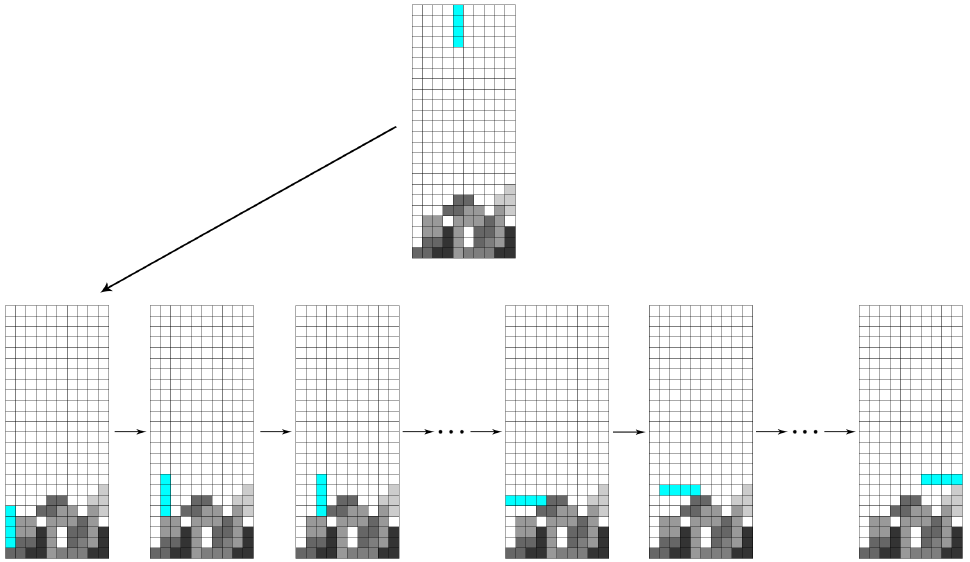
3.2. Scoring system#
The AI decides the best move by trying out all the possible ways (rotations and positions) of landing the falling tetromino. It computes a score for each possible move, and selects the one with the best score as its next move. As a consequence, the most crucial part of the AI is the scoring system. In order to survive as long as possible, the AI must be able to give a high score to the most favorably moves for the current tetromino. The score for each possible move is computed by assessing the grid the move would result in, based on a linear combination of four features:
where \(w_0, w_1, w_2, w_3\) are some positive weights.
The total height is the sum of the height of each column, that is the distance from the highest occupied tile in each column to the bottom of the grid. The AI wants to minimize this value, because a lower height means that more pieces can be dropped into the grid before hitting the top (and losing the game).

A complete line is a row with no holes. The AI wants to maximize them, because clearing lines makes more space for more pieces.

A hole is an empty space with at least one tile in the same column above it. The AI wants to minimize the number of holes, because they are harder to clear (all the lines above a hole must be clear before it can be filled up).
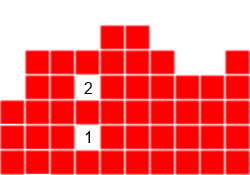
The bumpiness is the sum of the absolute difference in height between all two consecutive columns. The bumpiness measures the variation of its column heights. A big variation indicates the presence of wells, which are undesirable in a grid, because all the rows which the well spans are harder to clear. To ensure that the top of the grid is as monotone as possible, the AI wants to minimize this value.

3.3. Tetris AI#
The Tetris AI algorithm works as follows.
Enumerate the boards resulting from ALL possible placements (shifts and rotations) of the falling tetromino.
Calculate the score for each board.
Move the tetromino towards the position with the highest score.
One difficulty is that a tetromino cannot be instantly moved to the chosen position. At each step, the AI can only provide one of the following actions: Idle, Move left, Move right, Rotate left, Rotate right, Drop down.
3.4. Optimization of scoring weights#
Adjusting the tetris AI scoring weights can be formulated as an optimization problem. The goal is to find the values \({\bf w}=[w_0, w_1, w_2, w_3]\) that allow the tetris AI to maximize the number of complete lines. This can be mathematically written as
Of course, we don’t know the analytical expression of the function \(J_{\rm lines}\). We do know however how to evaluate this function on a given vector of parameters: we just need to play tetris using them as scoring weights. Derivative-free methods are particularly handy in this scenario, because they only require us to provide a mean to evaluate \(J_{\rm lines}\) with a python function! A noisy variant of the cross-entropy method is implemnted in this assignment to optimize the scoring weights. At the time of writing, this approach is considered the state-of-the-art for tetris.
3.5. Using better features#
The scoring system is the most important block of a tetris AI. Back in 2009, Christophe Thiery and Bruno Scherrer conducted an experimental study to identify the most effective set of features for the scoring system. Their findings are summarized in this research paper, for which there also exists a french version. The final part of this assignment is dedicated to implementing the eight features proposed by Thiery and Scherrer.
(Image taken from Amine Boumaza’s paper entitled “How to design good Tetris players”)
