4.6.2. Example 2

Consider this optimization problem involving a convex function of multiple variables

\[ \operatorname*{minimize}_{{\bf w}\in\mathbb{R}^N}\quad \frac{1}{2}\|A{\bf w}-{\bf b}\|^2 %J({\bf w}) = \frac{1}{2}\sum_{i=1}^P\big({\bf a}_i^\top {\bf w} - b_i\big)^2 = \frac{1}{2}\|A{\bf w}-{\bf b}\|^2 \]

where \(A\in \mathbb{R}^{P\times N}\) is a given matrix, and \({\bf b} \in \mathbb{R}^{P}\) is a given vector. Further assume that \(N=2\), \(P=3\), and

\[\begin{split} A = \begin{bmatrix} 1 & 2 \\ 3 & 2 \\ 2 & 1 \end{bmatrix} \qquad\qquad {\bf b} = \begin{bmatrix} 1 \\ -2 \\ 0 \end{bmatrix}. \end{split}\]

The cost function is displayed below.

4.6.2.1. Analytical approach

The quadratic function is one of the few cases when the minimum can be computed explicitly.

• First, derive the gradient of \(J({\bf w})\), that is

\[ \nabla J({\bf w}) = A^\top(A {\bf w} - {\bf b}). \]

• Then, solve the linear system that arises by setting the gradient to zero

\[ \nabla J({\bf w}) = \mathbf{0} \qquad\Leftrightarrow\qquad A^\top(A {\bf w} - {\bf b}) = \mathbf{0} \qquad\Leftrightarrow\qquad A^\top A {\bf w} = A^\top {\bf b}. \]

Assuming that \(A\) is full (column) rank, so that \(A^\top A \) is invertible, the above linear system is solved by

\[ {\bf\bar{w}} = \big(A^\top A\big)^{-1} A^\top {\bf b}. \]

This is the canonical solution to the least squares, which is well defined when the columns of \(A\) are linearly independent. In mathematical terms, this condition requires that \(P\ge N\) and \({\rm rank}(A)=N\).

4.6.2.2. Numerical approach

The solution to the least squares can be also found with gradient descent. As in the previous exemple, you need to

• implement the cost function with NumPy operations supported by Autograd,

• select the initial point, the step-size, and the number of iterations.

You are then ready to run gradient descent.

A = np.array([[1,2],[0,2], [2,1]])
b = np.array([1,-2, 0])

def cost_fun(w):
    return 0.5 * np.sum((A@w - b)**2)

init   = [-0.5,0.8]  # initial point
alpha  = 0.05        # step-size
epochs = 30          # number of iterations

w, history = gradient_descent(cost_fun, init, alpha, epochs)

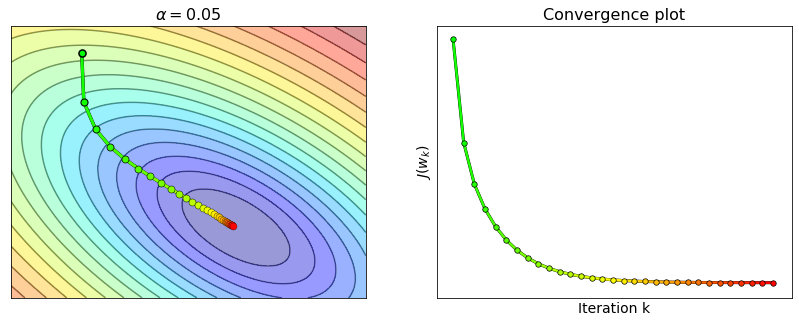
The figure below shows the process of optimizing the cost function with gradient descent. Instead of plotting a three-dimensional surface, the figure visualizes the two-dimensional contours of the cost function. Moreover, the sequence of points generated by gradient descent is marked on the contour plot with green dots at the beginning, with yellow dots as the algorithm converges, and with red dots toward the end. The same color scheme is used in the convergence plot. Remark that the convergence plot decreases and eventually flattens. This indicates that gradient descent converged to the minimum.